Altoparlanti e segnali impulsivi

Premessa.

Si può dimostrare facendo uso di complessi strumenti matematici che la risposta in frequenza e la risposta all'impulso di un sistema qualsiasi sono strettamente correlate fra loro.
E molti programmi di analisi acustica attualmente eseguono una misura del segnale riprodotto dal sistema sotto indagine, alimentato con un segnale multifrequenza che può essere un MLS (segnale quasi casuale contenente quasi tutte le frequenze) oppure un sinusoidale vobulato nella banda richiesta, oppure qualche altro tipo di segnale noto,  e producono contemporaneamente i due grafici della fig. 01.

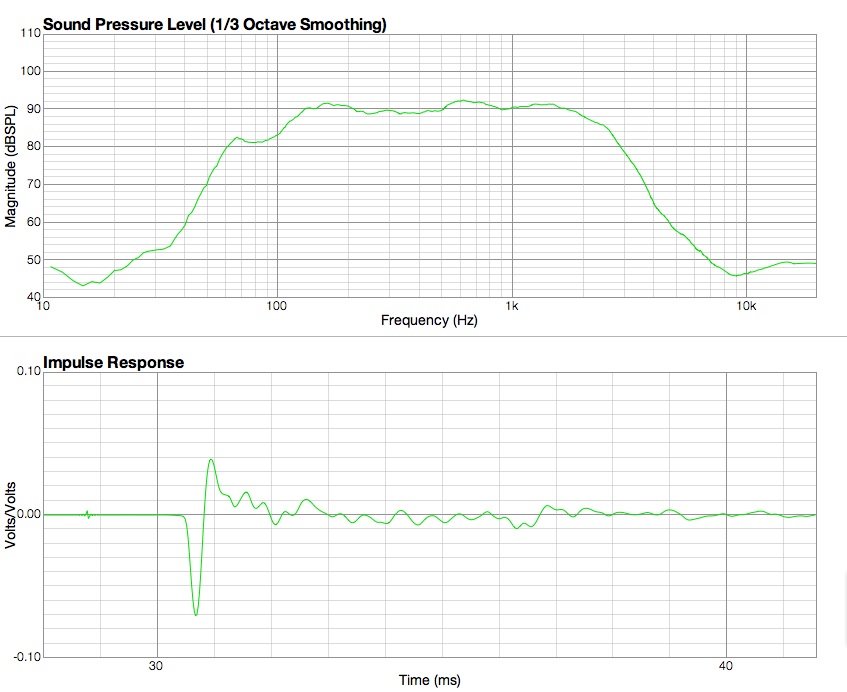
Fig. 01: grafici della risposta in frequenza e della risposta all'impulso di un woofer

I due grafici sono uno la trasformazione matematica dell'altro.

L'analisi dei sistemi in regime impulsivo è un ottimo metodo per capire il funzionamento dei sistemi sotto indagine.

Faceva notare Bartolomeo Aloia (in Costruire HiFi Num. 145, pag. 9) che ciò è talmente risaputo che   la fotocopia dei grafici originali (sono abbastanza sicuro che si riferisse a quello di Fig 02, tratto da AES Journal, Dicembre 1972, “Closed-box loudspeaker systems” e quello di Fig 03, tratto da AES Journal, Giugno 1973, “Vented Box loudspeaker systems” di R.H. Small ) è stata riproposta decine di volte senza che nessuno, o meglio quasi nessuno, si prendesse la briga di fare uno straccio di esperimento, che è per altro decisamente semplice da condurre.

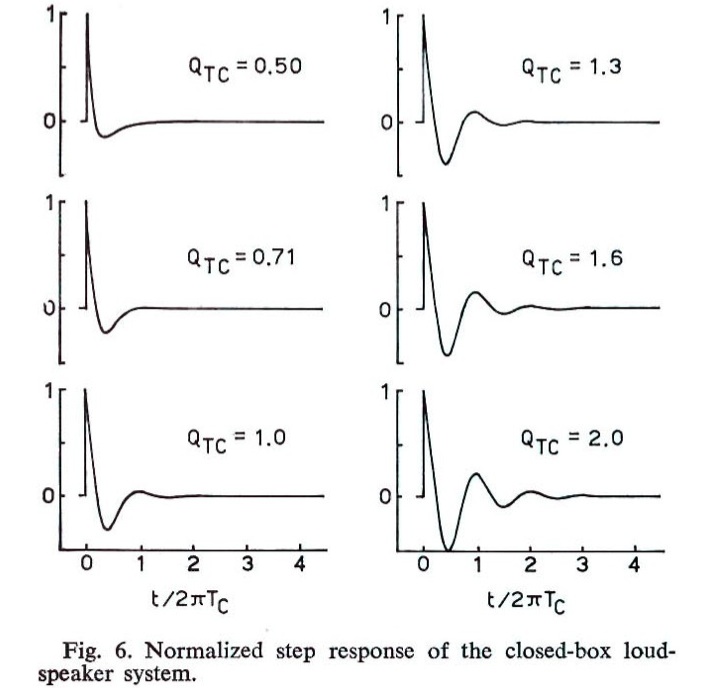
Fig. 02: Risposta all'impulso di un altoparlante in cassa chiusa (AES Journal, Dicembre 1972, “Closed-box loudspeaker systems”, R.H. Small)

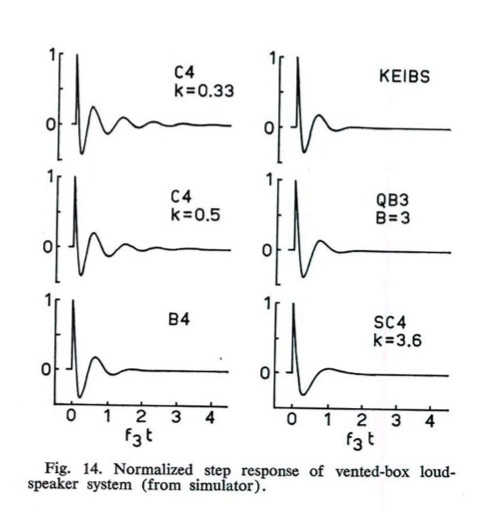
Fig. 03: Risposta all'impulso di un altoparlante in sistema Bass-Reflex (AES Journal, Giugno 1973, “Vented Box loudspeaker systems”, R.H. Small)

Per giunta quei grafici non derivano da una misura: al pari del grafico della risposta in frequenza al variare del fattore di merito, derivano da una simulazione al computer (1).  
Devo ammettere che anch'io ho citato quei grafici, in una pubblicazione divulgativa, per risparmiare tempo.

Però spesso non mi accontento delle simulazioni; intendiamoci, i simulatori sono uno strumento indispensabile per la progettazione, sia elettronica che acustica: senza Spice per progettare un circuito elettronico si dovrebbero fare un sacco di calcoli e spendere un sacco di tempo nel test e messa a punto, senza BASS-PC o AFW si dovrebbe.... costruire un prototipo in falegnameria e misurare.

Quindi  ho deciso di misurare la risposta di un altoparlante in regime impulsivo, perché io mi fido dei simulatori, e proprio perché so che in genere funzionano ma sono basati su approssimazioni e modelli, voglio capire bene quanto mi debbo fidare.

Il segnale e l'apparato sperimentale.

Un impulso dal punto di vista teorico è la Funzione δ (Delta) di Dirac, un segnale di ampiezza infinita, durata nulla che contiene tutte le frequenze.
È fisicamente non realizzabile, ma dato che deve pilotare un altoparlante che è un oggetto fisico, che come tale ha una risonanza propria, è abbastanza facile trovare una buona approssimazione di un impulso ideale.

Inoltre per questa misurazione, come sempre, non deve essere necessaria l'attrezzatura della NASA, sia perché non me la posso permettere, sia perché non dovendo rilevare l'undicesimo decimale della costante di gravitazione universale anche una attrezzatura più abbordabile, se usata in modo appropriato, può dare indicazioni significative.

L'altoparlante scelto per la prova è il Ciare CS160, un doppia bobina che ho già usato in altre misure.
In realtà qualsiasi altoparlante va bene, il CS160 va particolarmente bene perché ha un Qt di 0,55 (misurato) con le due bobine in serie e 0,99 (misurato) con una sola bobina quindi si presta a misure con Qt variabile senza troppe acrobazie.
Dulcis in fundo, sta lì sullo scaffale in attesa di essere utilizzato.

La risonanza del CS160 sta a circa 62 Hz, quindi il periodo intrinseco delle sue oscillazioni è di circa 16 ms.
Perché questa considerazione: perché l'altoparlante è un sistema oscillante, pertanto sottoposto ad una sollecitazione impulsiva si muove con tempi propri che dipendono dal suo periodo intrinseco.
Devo trovare una buona approssimazione di un impulso ideale, quindi devo produrre un segnale simil-impulso la cui durata sia trascurabile rispetto al periodo intrinseco dell'altoparlante.
In elettronica “trascurabile” significa concretamente: “differente per un ordine di grandezza”, quindi in questo caso la durata del segnale deve essere minore di 1,6 ms.
Per essere rilevabile all'oscilloscopio senza troppe acrobazie deve essere un segnale periodico, il cui periodo sia tale da consentire all'equipaggio mobile dell'altoparlante di tornare a riposo dopo l'oscillazione stimolata dall'impulso.
La soluzione è un'onda quadra a 5 Hz differenziata con un semplice filtro passa alto RC con un condensatore da 47 nF ed una resistenza da circa 6 kohm.
All'uscita del filtro troviamo un segnale che sale in un tempo trascurabile ed entro 1 ms è tornato a circa il 10% del valore di cresta.

Il filtro è in ingresso all'amplificatore da laboratorio che alimenta l'altoparlante.

Il movimento del cono viene rilevato con un semplice sensore ottico, lo stesso usato per rilevare la risposta dell'altoparlante ad un burst di onde sinusoidali (Interazioni, su questo sito).
È stato perfezionato con l'aggiunta di un buffer ed inscatolato per ridurre il rumore captato dal cavo, rumore che negli oscillogrammi dell'articolo "Interazioni" appare come una oscillazione residua nella zona di “silenzio” del burst.
La scelta del sensore ottico è dovuta al fatto che un microfono capterebbe tutte le riflessioni dell'ambiente, che sarebbero a circa 6 ms dall'impulso.
L'apparato di misura, in Fig 04, a parte il perfezionamento del sensore, è lo stesso dell'articolo "Interazioni", anche l'altoparlante è lo stesso.

Fig. 04: L'apparato sperimentale

Altoparlante in aria.

La prima serie di misure riguarda l'altoparlante in aria libera, che dal punto di vista concettuale è equivalente ad un altoparlante in box chiuso con Qts variabile, in quanto l'aria contenuta nel box contribuisce in prima approssimazione ad irrigidire la sospensione dell'altoparlante ma non modifica la struttura del sistema risonante.
La presenza del box contribuisce anche a modificare l'”air load” del cono, e di conseguenza la massa mobile effettiva, ma nemmeno questo cambia la struttura del sistema risonante, che rimane un oscillatore semplice formato da una massa ed una forza elastica.

Misurare la risposta all'impulso di un altoparlante con Qt variabile è facile, basta collegare in serie all'altoparlante una resistenza di valore opportuno e si ottiene qualsiasi valore di Qt maggiore di quello intrinseco dell'altoparlante.

Ho effettuato varie misure con le seguenti resistenze in serie, cui corrispondono i Qt:

Altoparlante con le bobine in serie (Qt base 0,55):

0 ohm        Qt = 0,55
1 ohm        Qt = 0,7
2,7 ohm    Qt = 1
4,7 ohm    Qt = 1,26
8,2 ohm    Qt = 1,5

Altoparlante con una bobina (Qt base 0,99):

8,2 ohm    Qt = 1,76

Nelle Figure da 04 a 09 si vedono gli oscillogrammi che mostrano lo spostamento del cono (traccia gialla) in corrispondenza all'impulso (traccia rossa).
L'impulso rilevato è in entrata all'amplificatore, non ai capi dell'altoparlante.

L'ampiezza dell'impulso varia in modo che l'ampiezza dello spostamento iniziale del cono sia sempre la stessa: la presenza della resistenza in serie all'altoparlante, per variare il Qt, rende necessario variare il segnale in ingresso per compensare la potenza persa nella resistenza e rendere confrontabili gli spostamenti del cono nelle diverse condizioni.

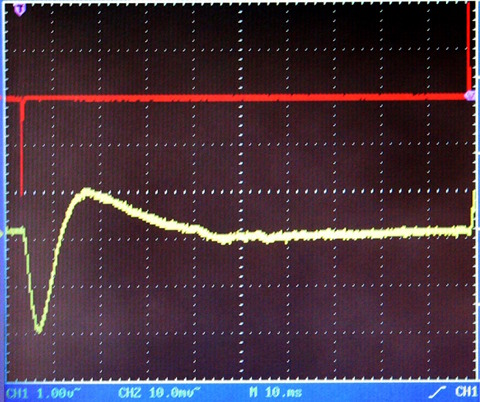
Fig. 05: Qt = 0,55

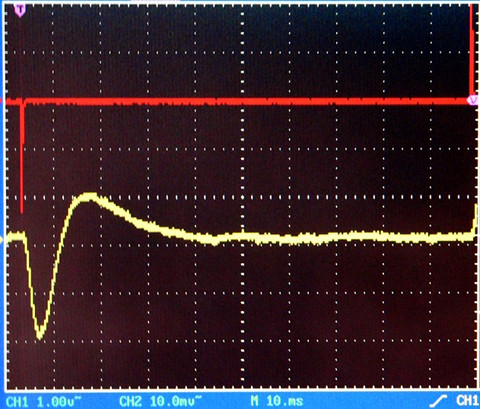
Fig. 06: Qt = 0,7

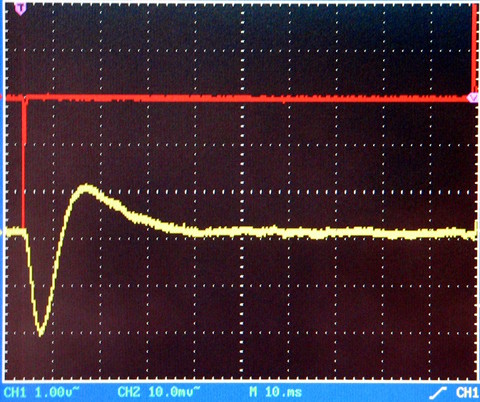
Fig. 07: Qt = 1

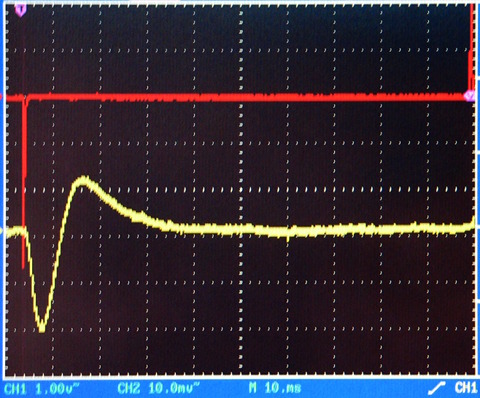
Fig. 08: Qt = 1,26

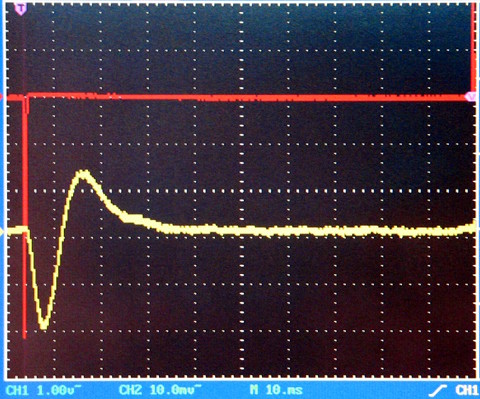
Fig. 09: Qt = 1,5

Fig. 10: Qt = 1,76

Che cosa si nota:
Gli impulsi sono alternati, positivo e negativo, essendo ricavati dalla differenziazione di un'onda quadra, e quindi corrispondono ai fronti d'onda in discesa ed in salita.
La durata dell'impulso è effettivamente trascurabile rispetto al movimento del cono, quindi il movimento del cono non è influenzato dal segnale elettrico (se mai il segnale elettrico viene influenzato dalla Back-EMF).
La distanza degli impulsi è tale che non esiste più movimento del cono rilevabile quando arriva l'impulso successivo (la base di tempi è 10 ms per divisione).

Ovviamente l'equipaggio mobile ha una massa, quindi una inerzia e pertanto non si muove con velocità infinita, come succederebbe ad un cono di inerzia nulla sollecitato da un impulso ideale.
Si muove con velocità finita e, aspetto più importante, essendo libero da sollecitazione, si muove con un moto che è essenzialmente sinusoidale smorzato.
Ovvio, trattandosi di un sistema elastico smorzato: sistema elastico in quanto il cono ha una massa e la sospensione una forza elastica, smorzato in quanto ci sono gli attriti meccanici e si muove in aria.
Il Qt rappresenta infatti lo smorzamento dovuto a tutti questi fattori.
Dato che il Qt è maggiore di 0,5 si innesca comunque l'oscillazione, come è chiaro dall'elongazione positiva che segue lo spostamento iniziale negativo.
Tutto come previsto dalla teoria dei sistemi oscillanti smorzati.
La distanza fra il picco negativo ed il picco positivo (un semiperiodo) è di circa (valutabile solo con approssimazione) 8 ms, che corrisponde ad una frequenza compresa fra 60 e 65 Hz, giusto la frequenza di risonanza del CS160, ed anche questo è in accordo con la teoria.

L'ampiezza del picco positivo, quello corrispondente alla oscillazione spontanea del cono in assenza di segnale, cresce con il Qt dell'altoparlante, cioè ad un minore smorzamento corrisponde una maggiore ampiezza delle oscillazioni innescate dall'impulso.
Per Qt maggiori di 1,5 l'oscillazione spontanea comincia a diventare significativa, appena percettibile in Fig.09 e vistosa in Fig.010.

Direi che c'è un buon accordo fra il dato sperimentale e la previsione teorica di fig. 02; il fatto che Fig.02 rappresenti in realtà la simulazione di una risposta ad un gradino anziché ad un impulso non cambia la sostanza.

Altoparlante con carico reflex.

Dopo la verifica in aria libera, il passo obbligato è vedere cosa succede se il carico dell'altoparlante è di tipo reflex.

Ho quindi realizzato un accordo reflex variabile, con un box da 30 litri che uso per effettuare misure sugli altoparlanti in box di volume ridotto (ad esempio la misura del Vas effettuata misurando la Fs in aria ed in box di volume noto), variando il volume interno mediante alcuni mattoncini di polistirolo a pori chiusi di volume noto, fissati con biadesivo.

Ho calcolato con BASS-PC un accordo QB3N4 (il QB3N1 non è possibile con un Qt di 0,55) ed un accordo B4.

Il QB3N4 dà 20 litri accordati a 48 Hz con un tubo da 58 mm lungo 130 mm.
Il B4 dà 28 litri accordati a 46 Hz con un tubo da 58 mm lungo 85 mm.

Ho quindi realizzato un pannello con il foro per l'altoparlante ed il tubo di lunghezza variabile, ottenuto con un tubo a sezioni giuntate con robusto nastro adesivo di tela.

Per la misura sul comportamento impulsivo del sistema reflex bisogna fare una premessa: il sensore ottico rileva solo lo spostamento del cono, e non tiene conto pertanto del contributo del condotto, che non è assolutamente trascurabile.
D'altra parte il contributo del condotto potrebbe essere rilevato solo da una misura acustica, che dovrebbe essere effettuata in camera anecoica (2).

Questo aspetto merita qualche ulteriore indagine che dovrà essere condotta con mezzi diversi, però presumo che il contributo del condotto possa essere di tipo additivo, non sottrattivo: il significato di questa considerazione è chiaro esaminando gli oscillogrammi dello spostamento del cono.

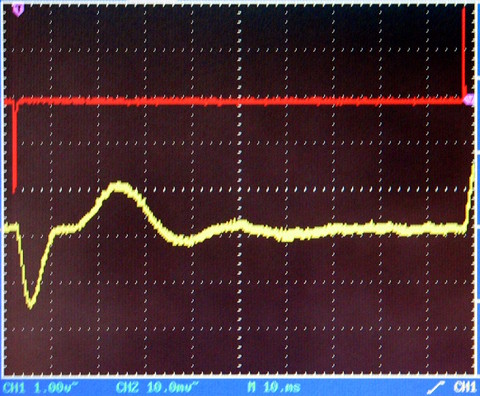
Fig. 11: Risposta all'impulso di un reflex QB3N4

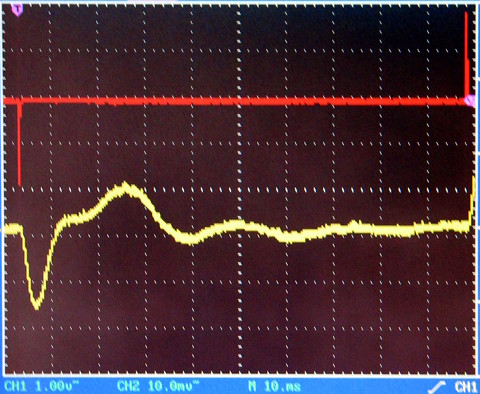
Fig. 12: Risposta all'impulso di un reflex B4

Dagli oscillogrammi di Fig. 11 (QB3N4) e Fig. 12 (B4) appare evidente che il movimento del cono è notevolmente diverso da quello del cono in aria.
Appare che c'è un sostanziale accordo con la simulazione di Fig 03, e la differenza potrebbe essere dovuta al contributo del condotto (la simulazione di Fig 03 tiene conto di tutto il flusso in uscita dal box, indipendentemente da quale apertura provenga).
La prima osservazione è che il cono si muove per un tempo molto più lungo dopo la cessazione dello stimolo.
La seconda osservazione è che il moto del cono non è semplicemente oscillatorio: dopo la semionda negativa iniziale, con caratteristiche analoghe a quelle del cono in aria,  appare esserci uno stop seguito da una seconda oscillazione che, dalla distanza fra il picco positivo ed il picco negativo (un semiperiodo) appare essere di frequenza più bassa della Fs dell'altoparlante e sembra essere abbastanza vicina alla frequenza di accordo del reflex.

Una ipotesi può essere che all'inizio il sistema risonante (il reflex è sostanzialmente un risuonatore di Helmholtz) influenzi il movimento del cono frenando bruscamente l'oscillazione innescata dall'impulso alla Fs, e successivamente l'aria del condotto in oscillazione lo muova alla sua frequenza di risonanza, la Fb.

È solo una ipotesi, da sottoporre ad ulteriori prove sperimentali con metodi diversi.


Conclusione.

Mentre per l'altoparlante in aria, e quindi con ottima approssimazione anche in box chiuso, la conclusione è semplice ed è una conferma sostanziale di quanto già si sapeva, per l'altoparlante in reflex in realtà non ho una conclusione pronta.
Posso dire che lo strumento più adatto di cui dispongo per valutare le prestazioni dei sistemi audio, il mio orecchio, mi dice che il comportamento dei due sistemi è notevolmente diverso, l'impulso riprodotto dall'altoparlante in aria è decisamente nitido, molto “secco” e decisamente povero di basse frequenze, mentre nel caso del reflex il suono è decisamente più corposo ed “allungato”, ricco di basse frequenze.
Però come ho detto nella premessa, la musica è un'altra cosa; nessun segnale musicale, nemmeno il suono delle percussioni, si avvicina se pur lontanamente ad un impulso come quello usato nel test.
In questi test l'altoparlante è sollecitato in un modo in cui non sarà mai sollecitato nemmeno da un colpo di cassa o di timpano.

L'indagine sul comportamento dei sistemi reflex deve essere condotta con metodo necessariamente acustico, e prosegue in "Altoparlanti e Segnali Impulsivi".




(1) Assicuro i più giovani che i computer esistevano e si usavano comunemente anche in quegli anni, erano un po' più ingombranti e molto più lenti, ma svolgevano il loro lavoro.
Io mi sono laureato proprio in quel periodo e nella mia tesi ho usato calcoli svolti al computer.

(2) In realtà ci può essere un altro metodo per rilevare la risposta a bassa frequenza di un sistema reflex tenendo conto anche del contributo del condotto, ed è la misura della pressione acustica eseguita all'interno del box, quindi sottoposta a doppia differenziazione e opportuno filtraggio, come descritto da R.H. Small in “Simplified Loudspeaker Measurements at Low Frequencies”, AES Convention Ottobre 1971.

La tecnica è però complessa e richiede una attrezzatura apposita calibrata in funzione del box; il tutto è ovviamente più semplice e più abbordabile di una camera anecoica adatta a rilevazioni a frequenze inferiori a un centinaio di Hz.
D'altra parte anche una misura a frequenze così basse in camera anecoica richiede una accurata calibrazione.
In futuro, forse.