|
Misurare l'impedenza degli
altoparlanti
Qualcuno potrebbe pensare che sulla
misura dell'impedenza degli altoparlanti sia già stato detto tutto.
Ma la scienza ci ha insegnato che su qualsiasi argomento non si ha mai
una conoscenza completa, e la conoscenza passa per la sperimentazione.
Fino
al 1600 era considerata verità incontrovertibile, anche presso
le persone di cultura, che i corpi cadessero perché “ogni
corpo tende al suo luogo naturale”, quindi i corpi materiali
tendono ad andare in basso mentre il fuoco sale.
Poi Newton ebbe l'intuizione della Legge di Gravitazione Universale che
formalizzò matematicamente ponendo che la forza attrattiva fra
due corpi qualsiasi (terra o aria non importa) è inversamente
proporzionale al quadrato della distanza che separa i due corpi, e per
400 anni questa fu la “verità”.
Einstein rivoluzionò la Fisica con la Teoria della
Relatività, che però risultò essere valida solo su
grande scala mentre a distanze subatomiche le forze si comportano
in modo totalmente diverso e ora, dopo meno di un secolo gli scienziati
sono alla ricerca di una Teoria Unificante (la “Teoria del
Tutto”) che sia in grado di rendere conto con un unico modello
sia della scala macroscopica sia della scala microscopica (a livello
sub-atomico), e di questa Teoria del Tutto sono stati proposti modelli
via via più sofisticati.
Nel campo dell'Elettroacustica la misura dell'impedenza è una
misura fondamentale perché dalla misura dell'impedenza in
funzione della frequenza si ricavano quasi tutti i parametri fisici di
un altoparlante, i parametri che servono al progetto di un diffusore,
quei parametri che si danno in pasto ai simulatori per ottenere le
caratteristiche della cassa da costruire.
Parecchio tempo fa Bartolomeo Aloia in uno dei suoi articoli magistrali
su Costruire HiFi, che Egli modestamente titola “Appunti di
Elettroacustica” (quella serie di articoli merita un attento studio),
mostrò sperimentalmente che esistono due metodi per la misura
dell'impedenza, uno detto “a tensione costante” e l'altro
detto “a corrente costante” (e in realtà in genere
si dovrebbe dire “quasi costante”) che non danno
risultati confrontabili.
In quell'articolo di Costruire HiFi, N. 145, a pag.16,
mostrò i risultati della misure e chiese perché le due
misure dessero una frequenza di risonanza diversa, ben oltre il normale
errore di misura (non intendo una misura fatta in modo errato, ma
l'errore statistico da cui sono affette tutte le misure effettuate con
strumenti reali), senza dare una risposta.
Nel numero successivo rilevò maliziosamente che nessuna risposta ancora
era stata data.
È
un dato di fatto che metodi di misura diversi danno risultati diversi,
e non si tratta solo di accuratezza degli strumenti, il problema
è concettuale.
Ma se metodi diversi danno risultati diversi quale è il metodo
“giusto”? E ancora, esiste il metodo “giusto”?
E si deve inoltre tener conto non solo del metodo ma anche delle
condizioni di misura, che influenzano il risultato almeno quanto il
metodo.
L'obiettivo di queste note non è dare la risposta assoluta, solo
sollevare un problema e suggerire alcune considerazioni per l'utilizzo
della strumentazione nel modo più proficuo.
Perché avere lo strumento più sofisticato serve a poco se
non sono chiari i concetti della fisica di base che si sta misurando
(spero che continuare a ripetere questo concetto non sia la solita
guerra persa).
Un
po' di storia
Prima di addentrarci nella teoria e nella sperimentazione è
opportuno riepilogare l'evoluzione delle tecniche di misura
dell'impedenza.
Nel 1954 la bibbia dell'acustica, “Acoustics” di Beranek
(qualcuno dirà “il solito Beranek”, ma da Beranek
non si può prescindere) illustra a pag. 229 un metodo di misura,
riportato in Fig.1, che è a corrente costante, in quanto la
tensione di uscita del generatore deve essere per ogni frequenza
regolata in modo che la tensione V2 ai capi di Rg sia costante.
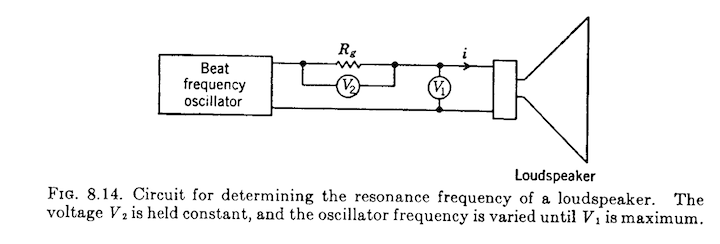
Fig.1
Misura dell'impedenza secondo Beranek
Nel 1958 Novak, nel suo storico
“Performance of Enclosures for
Low Resonance High Compliance Loudspeakers” (AES Library
6243) propone lo stesso metodo.
In entrambi i casi si tratta di un metodo a corrente veramente
costante, e la misura con l'apparato illustrato è
necessariamente una misura per piccoli segnali, dell'ordine di pochi
milliwatt.
Al contrario Neville Thiele nel 1962 (“Loudspeakers in Vented
Box”) propone la misura con il metodo a tensione costante, in
Fig.2.
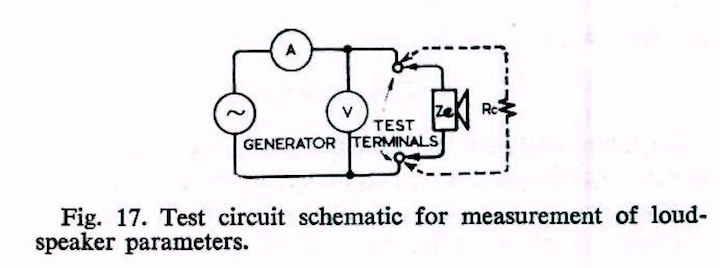
Fig.2
Misura dell'impedenza secondo Thiele
Richard Small circa 10 anni dopo
(“Direct Radiator Loudspeaker
System Analysis”, AES Library 7087) dice testualmente:
“Loudspeaker impedance measurements are
commonly taken with
either constant-voltage [….] or constant-current [….]
drive. If the driver is perfectly
linear or the measuring level is low enough
(il corsivo è mio nda), the two methods should give the same
result. The constant-voltage method has the advantage of more nearly
duplicating the usual operating conditions of the driver”.
Appare
evidente che le implicazioni sulla linearità e sul livello del
segnale di misura gli sono perfettamente presenti, ma non approfondisce
l'argomento in quanto la teoria per piccoli segnali era ancora in fase
di sviluppo e inserendo in quel momento ulteriori variabili non se ne
sarebbe più venuti a capo.
D'altra parte Harry Olson scrive in “
Elements of Acoustical Engineering”, Van Nostrand, 1940:
“... and should be capable of measuring the impedance at the full power output
of the speaker. The power input should be included with every impedance
characteristic. If the impedance characteristic varies with power
input, it is desirable to show a series of impedance frequency curves for
various inputs”
(il corsivo è mio nda), quindi è chiaro che il problema
della dipendenza della frequenza di risonanza dal livello del segnale
era ben noto.
Ho fatto questa premessa storica in quanto in molti testi divulgativi
più o meno recenti, in rete e anche come plug-in di qualche
software di misura (che non cito perché per tutte le altre
caratteristiche è assolutamente pregevole) viene proposto un
metodo a “corrente costante” semplificato, che riporto in
Fig.3.
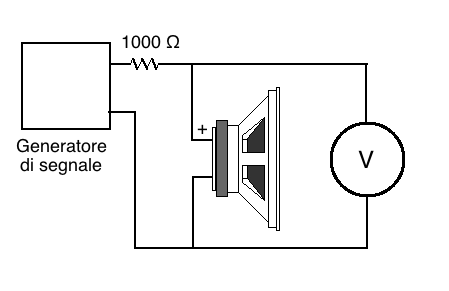
Fig.3
Misura dell'impedenza con metodo semplificato
Questo metodo semplificato consiste nel
rilevare la tensione ai capi di
un resistore di valore noto e prossimo all'impedenza nominale
dell'altoparlante, successivamente rilevare la tensione ai capi
dell'altoparlante e calcolare l'impedenza proporzionalmente al rapporto
fra le due tensioni, ovviamente la tensione del generatore è
indipendente dalla frequenza.
È evidente che la corrente in questo apparato non è
affatto costante, se il generatore, come dovrebbe, genera una tensione
costante al variare della frequenza.
Se con questo circuito misuro l'impedenza di un altoparlante HiFi o
comunque con fattore di merito meccanico non troppo elevato,
l'impedenza alla risonanza può essere dell'ordine di 40 o 50
ohm, quindi l'errore è entro il 5%, più che accettabile.
Ma se ho la pretesa di misurare l'impedenza di un altoparlante
professionale come ad esempio il CW328, la cui impedenza alla risonanza
è di circa 185 ohm, è chiaro che l'errore è
dell'ordine del 20%, decisamente troppo anche se sono interessato ad
una misura solo approssimativa.
Ma al di là dell'approssimazione dovuta ad un metodo rozzo, alla
quale si può rimediare con un po' di calcoli per i quali basta
un po' di pazienza e al giorno d'oggi un foglio elettronico, bisogna
capire se i metodi sono equivalenti o no.
Le misure riportate da Bartolomeo Aloia dimostrano che i due metodi non
sono equivalenti, e altre misure riportate negli stessi “Appunti
di Elettroacustica” dimostrano anche che la curva di impedenza
cambia sensibilmente con l'aumentare della potenza del segnale.
Sicuramente anche questo è noto, lo sapeva Olson nel 1940 e
hanno investigato a fondo su questo argomento Klippel e Clark negli
anni '90, i risultati sono stati pubblicati da entrambi nel 1999.
I due fenomeni, la dipendenza della curva di impedenza dal metodo di
misura e la dipendenza dal livello del segnale, non sono collegati,
dipendono da ragioni diverse, ma entrambi influenzano la curva di
impedenza che è quella curva che utilizziamo per determinate i
parametri di TS, quindi se parliamo di misurare l'impedenza degli
altoparlanti bisogna tener conto di entrambi.
E veniamo al dunque.
Quale metodo
e quali strumenti
Iniziamo con una considerazione: l'impedenza, non solo quella di un
altoparlante ma di qualunque dispositivo o sistema elettrico è
un concetto che potremmo definire “virtuale”.
Bartolomeo Aloia disse,
provocatoriamente, che l'impedenza non esiste.
Di
fatto l'Impedenza è una quantità fisica totalmente
diversa dalla Resistenza, dalla Capacità, dalla Induttanza: in
che senso è diversa?
Nel senso che mentre la Resistenza è
la caratteristica fisica dominante di un ben individuato componente, il
Resistore, la Capacità è la caratteristica fisica di un
ben individuato componente, il Condensatore, l'Induttanza è la
caratteristica fisica di un ben individuato componente, l'Induttore,
non esiste un componente specifico che ha come quantità
caratteristica l'Impedenza.
L'impedenza è una quantità fisica che descrive il
comportamento di un Sistema sotto l'effetto di uno stimolo oscillatorio.
L'Impedenza
di un altoparlante è la caratteristica che descrive il fatto che
una spira di conduttore che si muove in un campo magnetico genera una
corrente all'interno della spira.
Non importa che cosa faccia muovere la spira: può essere un'onda
acustica come nel caso di un microfono dinamico, può essere la
pressione del vapore che fa girare una turbina, come nel caso di un
generatore di una centrale elettrica, il fatto caratterizzante è
che in entrambi i casi la spira (meglio, le spire, molte) viene mossa
dentro un campo magnetico.
Nel caso dell'altoparlante ciò che muove la bobina mobile dentro
il campo magnetico è la corrente che l'amplificatore fa
circolare nelle bobina mobile stessa: la corrente genera il movimento
che a sua volta genera una corrente che è di segno opposto alla
corrente generata dall'amplificatore, e più la bobina mobile si
muove velocemente maggiore è la Forza Elettromotrice indotta,
che chiamiamo Forza contro-em.
Dato che è di segno opposto alla corrente che l'ha causata e
scorre nello stesso conduttore, la corrente totale diminuisce, e tanto
più diminuisce quanto maggiore è il movimento.
L'altoparlante
è un sistema meccanico risonante quindi alla frequenza di
risonanza il movimento è maggiore, la Forza contro-em è
maggiore e la corrente totale è minore.
È come se alla frequenza di risonanza all'amplificatore fosse
collegato un resistore di valore molto maggiore che alle altre
frequenze, ma la fisica sottostante è totalmente diversa, in
quanto un sistema risonante presenta anche un comportamento reattivo,
rappresentato dalla fase della corrente rispetto alla tensione.
Allora, che cosa significa realmente misurare l'impedenza, che cosa
stiamo misurando e di cosa dobbiamo tener conto nel caso specifico
dell'altoparlante?
Quale Metodo
Iniziamo dal metodo, che rivela un problema concettuale (l'osservazione
di R. Small sulle modalità correnti di utilizzo degli
altoparlanti è molto importante e deve essere ricordata).
Perché i due metodi, anche con segnali dello stesso livello, comunque
basso, danno un risultato diverso?
La risposta sta nel Circuito Equivalente Elettrico dell'altoparlante,
in Fig.4, e nel modo di rilevare l'impedenza.
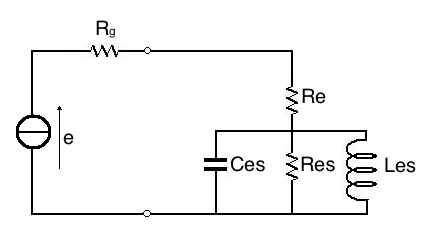
Fig.4
Circuito Equivalente Elettrico dell'altoparlante
In Fig.4 vediamo che dal punto di vista
elettrico l'altoparlante si
comporta come una rete RLC parallelo con in serie un resistore di
valore pari a Re (la
resistenza, in cc dato che si tratta di resistenza, della bobina
mobile).
L'amplificatore è rappresentato da un generatore ideale, con impedenza
di uscita nulla, con in serie una resistenza Rg,
che rappresenta l'impedenza di uscita dell'amplificatore cui si somma
la resistenza del cavo che collega l'altoparlante; alle basse frequenze
l'approssimazione che si compie sostituendo una resistenza
all'impedenza è minima.
Res è la
Resistenza elettrica equivalente alle perdite meccaniche (attrito,
viscosità, isteresi meccanica...) delle sospensioni, la
Capacità è l'equivalente elettrico della massa mobile,
l'Induttanza è l'equivalente elettrico della Cedevolezza delle
sospensioni (1).
Il circuito di Fig.4 è semplificato, in quanto ciò che ci
interessa è il comportamento nei dintorni della frequenza di
risonanza, che per un normale woofer o mid-woofer è inferiore a
100 Hz, quindi si è trascurata l'induttanza della bobina mobile,
che ha effetto ben al di sopra dei 100 Hz (a seconda del tipo di woofer
generalmente sopra 300 Hz).
Fig.4 rappresenta l'uso normale dell'altoparlante collegato ad un
amplificatore con impedenza di uscita Rg
molto bassa (nell'impedenza di uscita consideriamo anche il contributo
della resistenza in cc del cavo), nel caso di un normale amplificatore
con controreazione sicuramente trascurabile rispetto a Re.
Se osserviamo il sistema dal punto di vista della Forza contro-em,
vediamo cioè l'amplificatore dall'altoparlante, si può
osservare, in Fig.5, che alla Forza contro-em viene opposto un
carico composto da Re + Rg, in quanto un generatore ideale
ha impedenza nulla.
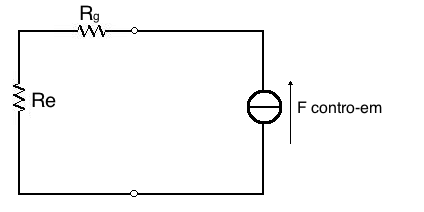
Fig.5
Circuito Equivalente Elettrico dell'altoparlante dal punto di vista
della Forza contro-elettromotrice
In queste condizioni è lecito
analizzare separatamente il
comportamento meccanico dell'altoparlante dal comportamento elettrico,
scomponendo il circuito di Fig.4 come in Fig. 6: Re costituisce lo smorzamento
elettrico del sistema risonante mentre Res
costituisce lo smorzamento meccanico.
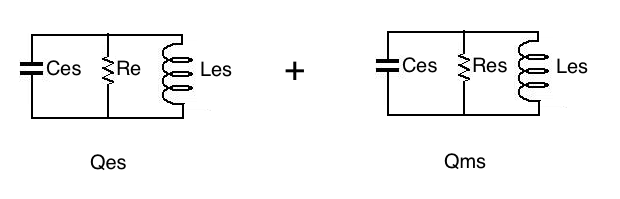
Fig.6
scomposizione del Circuito Equivalente nella parte meccanica e parte
elettrica
Se osserviamo la curva di impedenza di
qualsiasi altoparlante notiamo
immediatamente che lo smorzamento elettrico è molto maggiore
dello smorzamento meccanico, in quanto l'impedenza alla risonanza, che
coincide con la somma di Re e Res come è evidente dalla Fig.4, è
molto maggiore di Re, quindi Res è molto maggiore di Re.
L'utilizzo usuale di un altoparlante consiste nel collegare
l'altoparlante all'amplificatore con un cavo di resistenza molto bassa,
e appare chiaro che Rg ha
scarsa influenza sullo smorzamento elettrico, stante il suo valore
basso o trascurabile.
In un sistema risonante la frequenza di risonanza dipende dalle perdite
del sistema, meccaniche ed elettriche: in presenza di perdite la
frequenza di risonanza si abbassa e la curva di impedenza si allarga
(infatti il fattore di merito è la relazione fra la frequenza di
risonanza e la larghezza della curva).
Quando si misura l'impedenza con il metodo a tensione costante
l'apparato di misura è connesso esattamente così, con in
serie all'altoparlante un resistore di valore molto basso ai cui capi
si misura una tensione che è proporzionale alla corrente.
In pratica il resistore svolge la funzione dell'amperometro di Fig.2.
Quando si misura il fattore di merito
con il metodo a corrente costante il circuito di Fig.4 si trasforma
come in Fig.7, dove Rsc è il
resistore da 1000 ohm
(o più, in una vera misura a corrente costante sarebbe infinito) di
Fig.3.
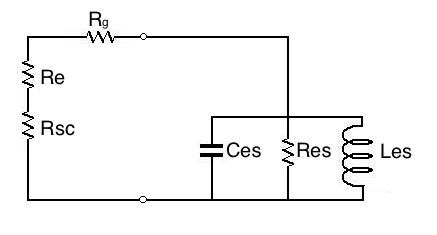
Fig.7
Circuito Equivalente Elettrico dell'altoparlante nella misura a
corrente (quasi) costante
È evidente che in questo caso lo
smorzamento elettrico è
totalmente diverso, molto minore, quindi la frequenza di risonanza
è maggiore di quella che si ha nel caso di Fig.4 e la larghezza
della curva di impedenza è minore (Q è maggiore).
Di fatto con questo valore di Rsc il sistema non è elettricamente
smorzato, e il valore di Qes
viene calcolato da Qms
solamente mediante un artificio matematico che è stato ricavato
presupponendo che Rsc non ci
sia.
Un altro
Metodo
È spesso usato, in dispositivi più sofisticati, un metodo
che io chiamo “misto”, rappresentato in Fig.8.
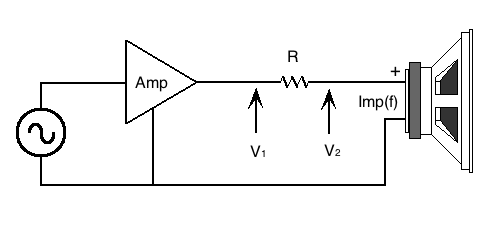
Fig.8 Misura
dell'impedenza con il metodo misto
Metodo “misto” in quanto il resistore
in serie
all'altoparlante ha un valore confrontabile con l'impedenza nominale
dell'altoparlante, ad esempio 10 ohm.
Con un valore così basso lo smorzamento
elettrico viene alterato in misura che si presume calcolabile.
Misurando V1(f) e V2(f) l'impedenza può essere calcolata come:
Z(f) = R * V2(f) / (V1(f) – V2(f))
infatti (V1(f) – V2(f)) / R misura la corrente che scorre
nell'altoparlante.
Questo metodo viene utilizzato da Speaker Workshop, per il quale vi
rinvio agli articoli di
Claudio Negro e da ARTA,
per il quale vi rinvio all'ottimo manuale che trovate in rete.
Speaker Workshop può essere utilizzato sia direttamente dalla
scheda audio, se questa ha una uscita sufficiente a pilotare una
cuffia, oppure con un amplificatore di potenza attenuando
opportunamente i segnali che tornano alla scheda audio.
Per ARTA il manuale suggerisce sempre
l'utilizzo di un amplificatore
esterno per effettuare le misure con una potenza non irrisoria, almeno
1 W.
Per entrambi è necessario costruire una interfaccia esterna, in
entrambi i casi costruttivamente semplice, nel caso di ARTA il
resistore R deve essere in grado di dissipare una potenza elevata.
Entrambi richiedono una calibrazione preventiva per effettuare misure
attendibili.
Entrambi i programmi sono per ambiente Windows.
Io uso Speaker Workshop da tempo con la sua interfaccia (jig per
“soci del club”) per le misure di impedenza (e anche per
rilevare le curve di risposta delle casse reflex con la tecnica
“in campo vicino” in quanto la fusione della risposta del
cono e del o dei condotti è automatizzata).
Per altre misure elettriche e acustiche uso Fuzz Measure, un programma
per Mac.
Il mio “super
jig”
Per effettuare misure elettriche ed acustiche assistite dal computer ho
costruito un “marchingegno” che:
- assicurasse la massima flessibilità di
ingressi e uscite per livello e attenuazione dei segnali
- avesse sul pannello anteriore tutti di
connettori: XLR e TRS con
segnale bilanciato, BNC con segnale sbilanciato eliminando la
necessità di adattatori
- raggruppasse in un unico strumento
tutti i dispositivi che mi
permettessero di effettuare qualsiasi (quasi, ovviamente) tipo di
misura con la massima sicurezza per la scheda audio (è troppo
facile distruggerla inavvertitamente se si misura la risposta di un
amplificatore da 300 W)
Il “marchingegno” comprende in un unico involucro due canali di
ingresso e due di uscita ripresi pari pari dal Jig di P. Millet,
e un amplificatore di potenza (50 W su 8 ohm) con qualche circuito
ausiliario per alimentare direttamente un altoparlante oppure
effettuare sia misure di impedenza con il metodo misto sia a tensione
costante.

Fig.9
il mio super jig
In Fig.9 l'interno del mio super jig;
non descrivo le parti relative
all'ingresso e all'uscita in quanto corrispondono esattamente al super
jig di Claudio Negro; l'unica differenza è che, dato che lavoro
molto con sistemi a linee bilanciate gli attenuatori di ingresso sono
realmente bilanciati e, per ridurre al minimo gli effetti delle
capacità disperse, i resistori del partitore (film metallico a
0,1% di tolleranza) non sono sulla basetta ma sono saldati a ridosso
dei contatti del commutatore (Fig. 10), soluzione poco elegante ma
assolutamente efficace, la stessa tecnica che veniva usata negli
strumenti quando non esistevano i circuiti stampati.

Fig.10
partitori di ingresso del super jig
L'amplificatore di potenza è il solito
(per me) circuito basato su LM3886, kit di
Futura Elettronica
lievemente modificato per estendere a pochi Hz la risposta in frequenza
verso il basso; l'ho usato in varie occasioni ed ha sempre funzionato
perfettamente quindi continuerò ad adottarlo quando
servirà.
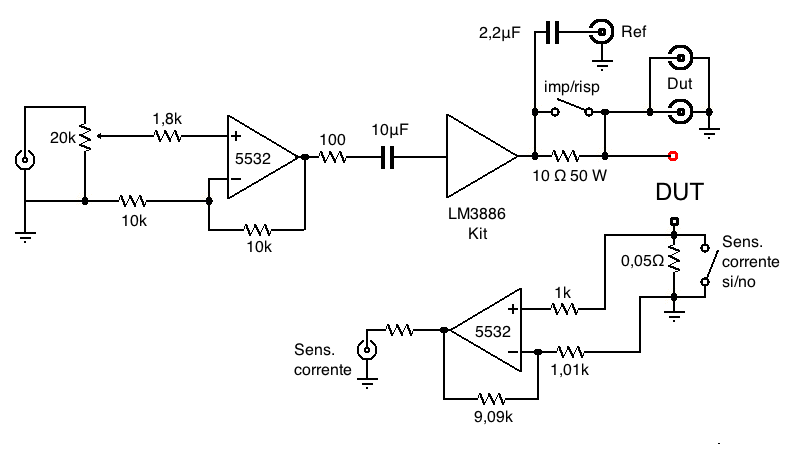
Fig.11
schema elettrico dello stadio amplificazione
Lo schema della parte amplificatore è
in Fig.11.
In Fig.12 il pannello anteriore: si nota immediatamente che le tre
parti sono totalmente indipendenti: questo dà la più
totale flessibilità nella configurazione del dispositivo per
effettuare tutti i tipi di misure.

Fig.12
pannello anteriore del super jig
I vari stadi vengono collegati secondo
necessità con corti
cavetti terminati da connettori BNC: questa soluzione, che sembra poco
elegante, è invece molto funzionale in quanto consente di
evitare una matrice di commutatori che sarebbe stata troppo complessa
per usare il jig in tutti i modi possibili e poco efficace dal punto di
vista del rumore e dei loop di massa; soluzione per altro ispirata dal Sistema Clio.
Le
misure
Ho quindi effettuato una serie di misure sul sub woofer Ciare CS160,
con le bobine in serie.
1. Una misura con Speaker Workshop, quindi metodo misto, con il jig
standard (senza amplificazione, usando solo la scheda audio), con il
quale ho anche effettuato la calibrazione.
2. Una serie di misure con Speaker Workshop con il super jig, usando
l'amplificatore di potenza a vari livelli e attenuando il segnale di
ritorno nella stessa misura dell'amplificazione applicata di volta in
volta, in modo che la calibrazione rimanesse valida. Queste misure sono
effettuate con il metodo “misto” proprio di Speaker
Workshop.
3. Una serie di misure con Fuzz Measure con il super jig,
metodo a tensione costante, a vari livelli di potenza con
corrispondente attenuazione del segnale di ritorno al computer.
In Fig.13 la misura a tensione costante: si vedono le curve prodotte da
Fuzz Measure, il super jig con i collegamenti esterni fra i tre moduli
e, sopra il super jig un multimetro analizzatore a 5 cifre e ½ ,
con calibrazione certificata, per controllare il segnale che arriva ai
capi dell'altoparlante.
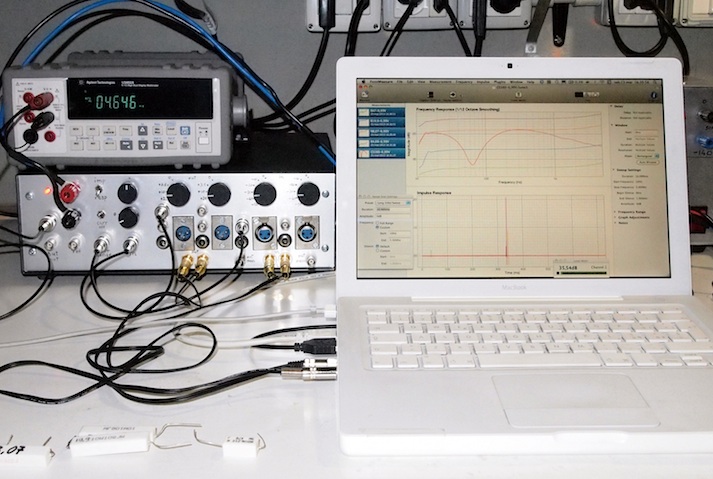
Fig.13
misura a tensione costante
L'analizzatore nella funzione “Volt AC
RMS” è stato
usato anche con Speaker Workshop, per controllare la potenza applicata
all'altoparlante.
Ho usato un analizzatore a “valore RMS vero” in quanto come
vedremo nell'analisi delle misure, Speaker Workshop e Fuzz Measure
usano segnali di natura completamente diversa per effettuare le misure
e un normale multimetro non avrebbe dato valori attendibili.
L'analizzatore è certificato per misurare il valore RMS vero di
qualsiasi tipo di segnale fra 5 Hz e almeno 100 kHz.
Le misure con Speaker Workshop
Speaker Workshop misura l'impedenza dell'altoparlante mediante un
segnale a larga banda, simile ad un rumore termico ma generato da un
algoritmo matematico.
All'ascolto appare come un soffio, di durata pari a una decina di
secondi (dipende dal numero di ripetizioni impostate).
Questo segnale contiene nello spettro definito della misura (ho
definito da 20 Hz a 20 kHz) un insieme molto elevato di frequenze di
ampiezza ridotta.
Non è un vero rumore termico, essendo generato con un algoritmo
matematico, quindi non contiene tutte le frequenze random, è un
segnale pseudo-casuale che contiene un insieme di frequenze molto
elevato ma definito e limitato dall'algoritmo di generazione.
La prima misura è fatta con il jig “standard” di
Speaker Workshop senza amplificatore: l'ampiezza del segnale ai capi
dell'altoparlante è di 331 mV RMS, il livello del segnale
è quello che non provoca saturazione dei circuiti di ingresso e
di uscita della scheda audio; la determinazione di questo livello viene
effettuata durante la procedura di calibrazione, i livelli e le
impostazioni vengono memorizzati in un apposito file per essere
richiamati quando servono.
Speaker Workshop esegue la misura confrontando il segnale sul canale
destro con il segnale del canale sinistro, quindi non è
importante che il segnale sia esattamente a quel livello, l'importante
è non superare quel livello perché è più o
meno il massimo possibile senza saturazione; il livello dipende
comunque dal computer e dalla scheda audio, con hardware diverso
sarà diverso.
Speaker Workshop misura l'impedenza e dai dati memorizzati
dell'impedenza in funzione della frequenza, dopo aver fornito Re e Sd,
è in grado di stimare alcuni parametri di Thiele e Small;
l'obiettivo di questa misura era esclusivamente rilevare la frequenza
di risonanza e i fattori di merito, gli altri parametri non sono quindi
stimati ma non sono rilevanti per il nostro obiettivo.
In Fig.14 e 15 la curva dell'impedenza
e la stima dei parametri
eseguita senza amplificazione a basso livello: 331 mV su 8 ohm
equivalgono a 13,7 mW.
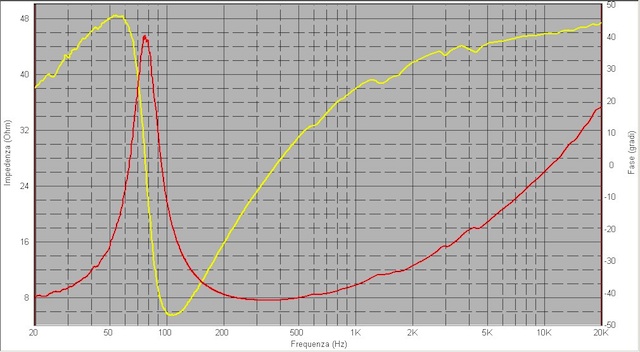
Fig.14
curva di impedenza misurata da Speaker Workshop con il jig standard
(senza amplificazione) a 331 mV RMS

Fig.15
stima dei Parametri TS effettuata da SpeakerWorkshop
Ho quindi inserito il super jig con gli
opportuni collegamenti ed
eseguita la misura con l'amplificatore impostato per rilevare ai capi
dell'altoparlante 310 mV (mi è stato impossibile impostare il
controllo di guadagno dell'amplificatore in modo da riprodurre i 331
mV, ma ritengo l'approssimazione più che accettabile), che
corrispondono a 12 mW.
L'attenuatore di ingresso è a 0 dB, riproduce il funzionamento del jig
standard.
In Fig16 la curva rilevata in queste condizioni, perfettamente
sovrapponibile a quella precedente, quindi la calibrazione risulta OK.
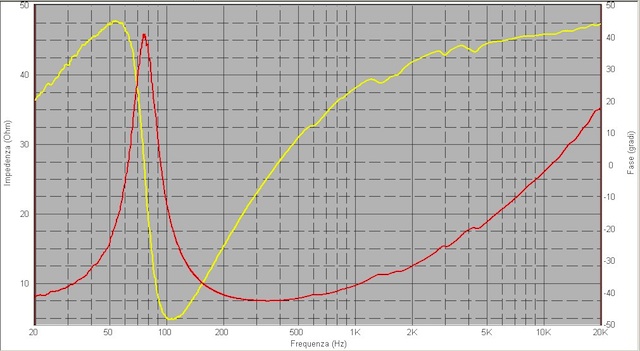
Fig.16 curva di
impedenza misurata da Speaker Workshop con il super jig a 310 mV RMS
In Fig.17 e 18 la curva e i parametri
stimati con il guadagno
dell'amplificatore regolato per avere 2,84 V RMS, 1 W
nominale, ai capi dell'altoparlante e attenuatore di ingresso a
-20 dB, all'ingresso risultano 284 mV quindi la misura è
effettuata, dal punto di vista di Speaker Workshop come se fosse
collegato il jig standard senza amplificazione.
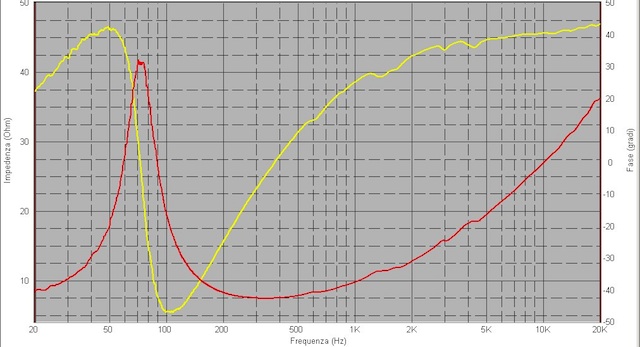
Fig.17
curva di impedenza misurata da Speaker Workshop con il super jig a 2,84
V RMS

Fig.18
stima dei Parametri TS effettuata da SpeakerWorkshop a 2,84 V RMS
In Fig.19 la curva di impedenza
rilevata con 7,05 V RMS, 6,1 W nominali, e attenuatore a – 30 db.
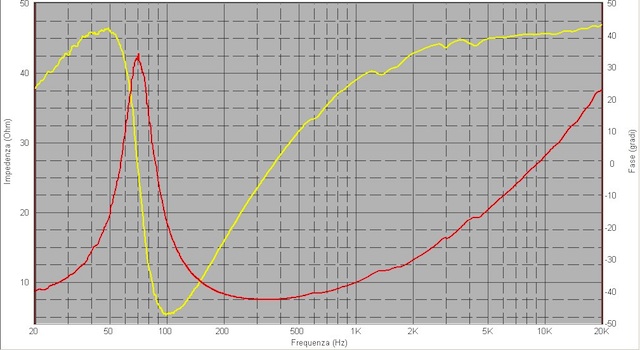
Fig.19
curva di impedenza misurata da Speaker Workshop con il super jig a 7,05
V RMS
In Fig. 20 e 21 la curva di impedenza e
i parametri stimati,
rilevazione con con 12,06 V RMS, 18 W nominali, e attenuatore a
– 40 db.
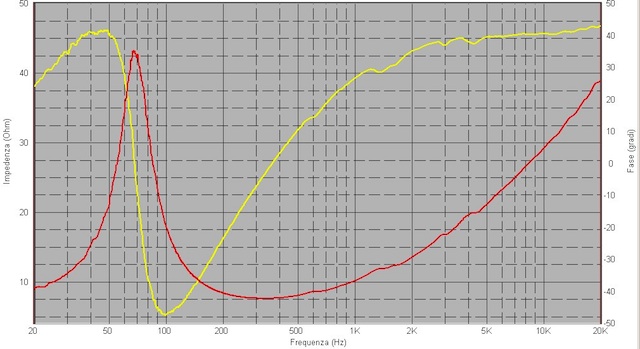
Fig.20
curva di impedenza misurata da Speaker Workshop con il super jig a
12,06 V RMS

Fig.21
stima dei Parametri TS effettuata da SpeakerWorkshop a 12,06 V RMS
Le misure con
Fuzz Measure
Fuzz Measure esegue le misure con un segnale sinusoidale vobulato
(sweep), un segnale sinusoidale monofrequenza la cui frequenza varia da
un minimo a un massimo impostati nei parametri di vobulazione.
Il segnale è completamente diverso da un segnale a larga banda
pseudo casuale, in quanto contiene ad ogni istante una unica frequenza.
Quindi ad ogni istante abbiamo un segnale la cui ampiezza è
quella rilevata dall'analizzatore e non la somma di n
segnali di ampiezza molto più bassa.
Questo durante la prova si sente, l'altoparlante sotto test non emette
un soffio ma un segnale continuo di frequenza variabile, e si vede
osservando l'escursione del cono, che alle frequenze basse è
chiaramente visibile ad occhio nudo anche a basso livello e diventa
impercettibile quando la frequenza raggiunge la gamma in cui il moto
del diaframma è controllata dalla massa, quindi dall'inerzia, e
pertanto inversamente proporzionale alla frequenza stessa.
Con questo tipo di segnale alle frequenze basse, soprattutto nelle
vicinanze della frequenza di risonanza, non è possibile eseguire
la misura con una potenza elevata quanto con un segnale a larga banda,
nel quale la potenza è distribuita su una gamma molto ampia e
pertanto i singoli segnali hanno livello molto più basso; quanto
più basso non so dire con esattezza perché dipende dalla
costituzione del segnale a larga banda e non conosco l'algoritmo di
generazione di Speaker Workshop; dall'escursione dell'altoparlante
posso ipotizzare da 15 a 20 dB più bassa (è una stima
veramente brutale).
Ho concluso la misura con 7 V RMS e già a questo livello
l'escursione del cono era ampiamente superiore alla Escursione massima
lineare ( Xmax ), benché ancora inferiore ma credo di poco
all'escursione meccanica massima.
La misura a tensione costante misura la corrente che passa nella bobina
mobile, quindi il grafico direttamente prodotto dal programma è
inverso rispetto a quello prodotto da Speaker Workshop.
Fuzz Measure misura il livello in dB del segnale ai capi della
resistenza del valore di 0,05 ohm (nel mio super jig) in serie
all'altoparlante, e produce a richiesta un file .csv contenente le
frequenze rilevate e il livello in dB corrispondente, in Fig.22.
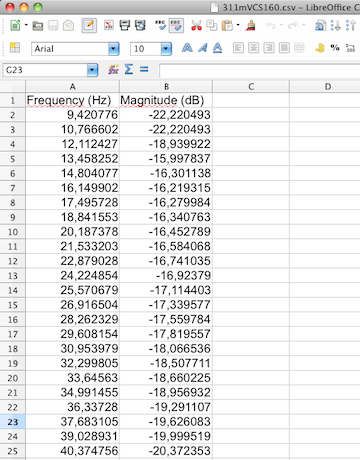
Fig.22
esempio di file .csv prodotto da FuzzMeasure
Ho eseguito le misure a circa gli
stessi livelli RMS rilevati con
Speaker Workshop, fermando il test a 7 V per il motivo spiegato.
In Fig.23 la misura a 311 mV RMS, attenuatore di ingresso a 0 dB; la
curva rossa indica la corrente nella bobina mobile, le quasi rette
orizzontali indicano le rilevazioni fatte con resistori di valori
diversi, usati per calibrare il sistema, cioè avere un
riferimento certo delle impedenze in gioco.
La risonanza è a 71,33 Hz.
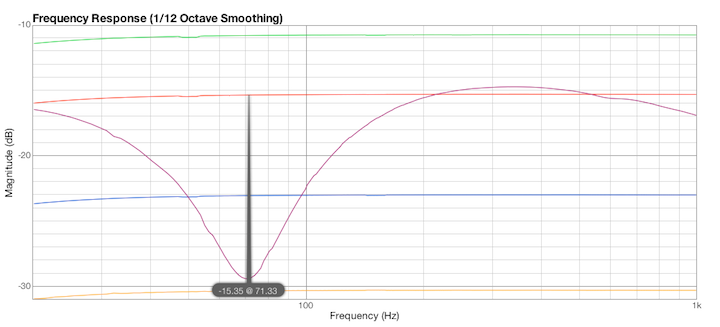
Fig.23
misura eseguita con FuzzMeasure a 311 mV RMS
I resistori si vedono in Fig.13 a
sinistra in basso; il loro valore
effettivo a temperatura ambiente è stato misurato con
l'analizzatore nella funzione “Resistenza a 4 fili”, per
scrupolo; precauzione inutile in quanto i 10 secondi delle misure a
potenza più alta sono sufficienti ad aumentarne la temperatura
in misura percettibile.
I valori dei resistori sono 4,69 ohm, 8,21 ohm, 19,9 ohm, 47 ohm ;
l'analizzatore fornisce un numero di decimali molto superiore, del
tutto privo di significato in questa misura.
Per ogni resistenza è stato ricavato il file .csv.
Nel
grafico di Fig.23 ai valori dei resistori 4,69 ohm, 8,21
ohm, 19,9 ohm, 47 ohm dorrispondono rispettivamente le curve
verde, rossa, blu,
gialla.
I files .csv trasferiti in un
foglio di calcolo e sottoposti ad
un semplice algoritmo si trasformano nella curva di impedenza normale,
il files corrispondenti ai resistori noti servono ad aggiustare i
coefficienti dell'algoritmo per calibrare la curva.
In Fig.24 il risultato finale del grafico di impedenza, “raddrizzato”,
per il segnale a 311 mV RMS.
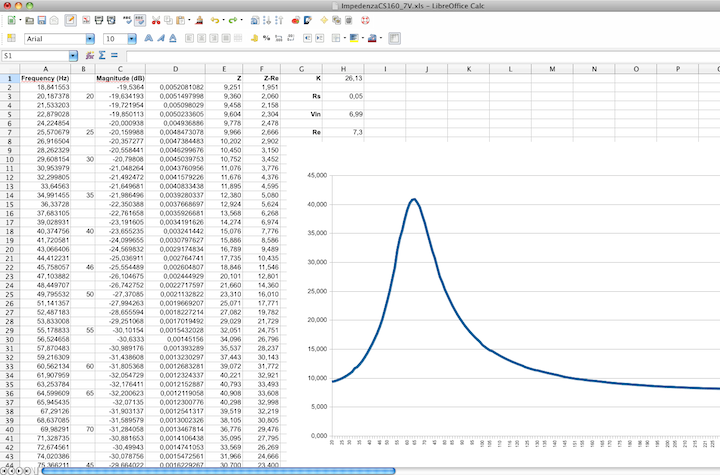
Fig.24
grafico di impedenza in forma normale
In Fig.25 il grafico di FuzzMeasure,
per il segnale a 2,84 V RMS, attenuatore di ingresso a -20 dB.
La risonanza è a 64,6 Hz.
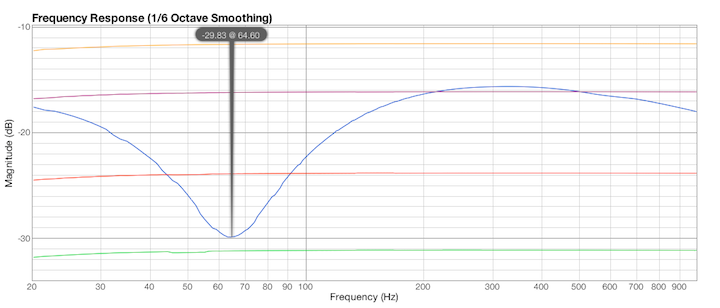
Fig.25
misura eseguita con FuzzMeasure a 2,84 V RMS
In Fig.26 il grafico di FuzzMeasure,
per il segnale a 6,99 V RMS, attenuatore di ingresso a -30 dB.
La risonanza è a 63,25 Hz.
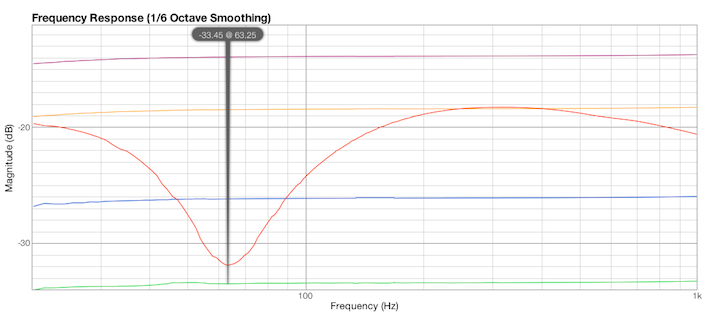
Fig.26
misura eseguita con FuzzMeasure a 6,99 V RMS
Appare chiaro che la sollecitazione
dell'altoparlante è molto
maggiore, infatti la frequenza di risonanza è più bassa
che per equivalenti livelli di potenza con segnale a larga banda, e
pertanto la frequenza di risonanza dipende dall'escursione e non
direttamente dalla potenza applicata.
La misura è stata eseguita con un dispositivo costruito
appositamente, e non c'è quindi la possibilità di
produrre automaticamente una stima dei parametri.
Il foglio di calcolo contiene però i valori di impedenza
calcolati dalla misura di ampiezza, misurati con una risoluzione di 1,4
Hz, quindi è possibile rilevare la frequenza di risonanza con
buona precisione e calcolare i Fattori di merito dalle caratteristiche
della curva.
In qualsiasi sistema risonante il fattore di merito Q è dato, se
il sistema non è sovrasmorzato, dalla larghezza di banda, la
definizione standard di Q
basata sulla larghezza di banda (2) è
la seguente:
Q = fs / (fh – fl)
dove fh e fl sono le due frequenze alle quali
la risposta è a -3 dB rispetto al picco e vale la relazione:
fs = radq(fl * fh) ( radq() è la
radice quadrata).
Nel foglio elettronico si sottrae quindi Re dalla curva di impedenza
per ottenere Res(f), in colonna F di Fig.24, e si determinano quindi le
due frequenze alle quali l'impedenza è (Zmax – Re) /
1,4142; in questo modo, operando solo su Res, si ricava Qms.
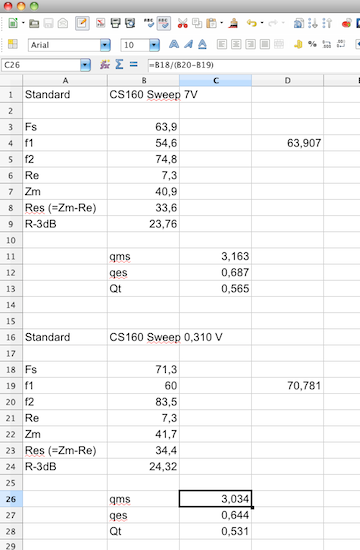
Fig.27
calcolo dei fattori Q
Con un altro semplicissimo foglio di
calcolo che applica la precedente
formula di Q, in Fig.27, si
ottiene Qms; applicando
la teoria
standard di Thiele e Small con la formula:
Qes = Qms / (Zmax/Re - 1)
si calcola Qes e infine da Qms e Qes si ottiene Qt.
In Fig.27 si vedono i risultati calcolati con 311 mV e 6,99 V RMS.
In questo calcolo ho usato la teoria standard del Q, rilevando i punti
a -3 dB; ciò è agevole per altoparlanti con Qms non molto
elevato, in quanto la curva di impedenza risulta sufficientemente larga
da poter rilevare i punti a -3 dB con ragionevole approssimazione,
eseguendo una interpolazione lineare sui lati della curva, che non
risultano eccessivamente ripidi e quindi la larghezza di banda non
è troppo ridotta rispetto a fs.
Nel caso di un altoparlante di tipo
diverso, quale ad esempio il CW328,
che ha una fs di circa 50 Hz e
un Qms pari a 15, la larghezza
di banda
risulterebbe di 3,33 Hz, confrontabile con la risoluzione della misura.
In questo caso R.H. Small suggerisce di rilevare i punti in cui il
valore è:
Z = radq(Zmax * Re)
che stanno a circa -18 dB, e applicare un fattore correttivo alla
formula standard del Q.
La larghezza di banda è in questo caso molto maggiore e quindi
meno influenzata dalla risoluzione della misura; con altoparlanti a
basso Qms ciò potrebbe portare
fh troppo vicina alla
seconda
risonanza e quindi risentire dell'effetto di Le e delle Eddy Currents;
a mio parere quale larghezza di banda utilizzare deve essere deciso di
volta in volta a seconda del tipo di altoparlante.
Considerazioni sull'uso dei due metodi
Il metodo misto di Speaker Workshop produce con l'aumento della potenza
applicata una frequenza di risonanza che diminuisce e un fattore di
merito che diminuisce.
Il metodo a tensione costante produce con l'aumento della potenza
applicata una frequenza di risonanza che diminuisce e un fattore di
merito che aumenta.
A basso livello, tenendo conto del fatto che con il segnale vobulato
l'altoparlante subisce una sollecitazione maggiore, i dati forniti dai
due metodi appaiono abbastanza congruenti: Speaker Workshop fornisce fs
= 77,5 Hz e Qts = 0,552 mentre
Il metodo a tensione costante fornisce fs
= 71,3 Hz e Qts = 0,53.
La differenza in fs è coerente
con il diverso segnale e la
differenza di 0,022 in Qts può agevolmente rientrare nell'errore
di misura.
I valori di Qts calcolati con
il metodo a tensione costante derivano da
valori elementari di ampiezza e frequenza ricavati da un metodo
automatizzato ma che potrebbero con un po' di pazienza essere ricavati
manualmente; i valori di impedenza calcolati dai dati sono
ragionevolmente attendibili in quanto confrontati con resistori di
valore noto.
D'altra parte l'aumento di Qts
con l'escursione del cono è
coerente con tutte le misure condotte con il Sistema di Klippel che io
ho finora visto.
In Fig.28 i diagrammi fondamentali di Klippel cortesemente prodotti da
Mattia d'Antonio della Ciare su mia richiesta su un woofwer PW252.
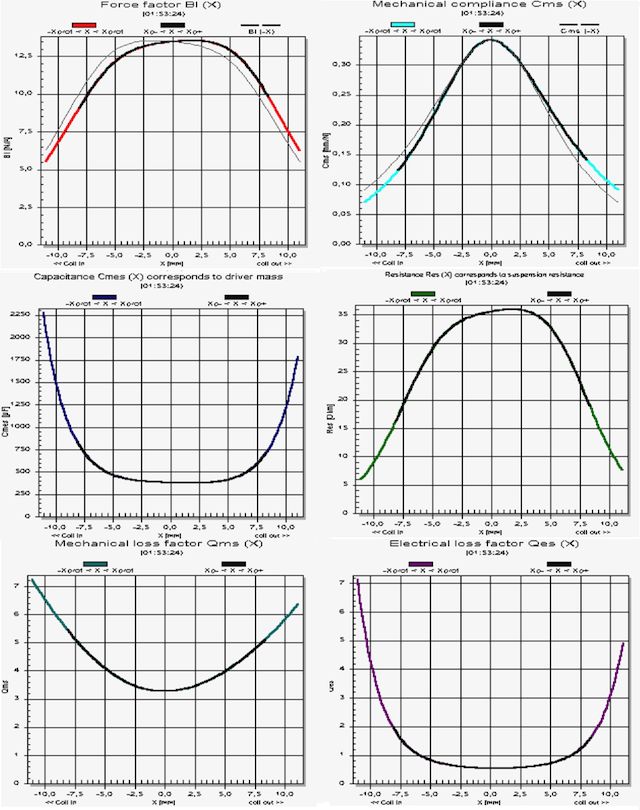
Fig.28
diagrammi di Klippel di un PW252
Negli articoli “L'altoparlante, questo
sconosciuto”
pubblicati nei N 81 e 82 di Costruire HiFi Giuliano Nicoletti presenta
i grafici di Klippel rilevati su tre diversi altoparlanti.
Nei fogli tecnici di tutti gli altoparlanti SICA (un produttore
italiano di altoparlanti professionali, www.sica.it) sono riportati
anche alcuni grafici di Klippel.
In tutti questi casi appare chiaro che il comportamento specifico di
Qts in funzione dell'escursione del cono dipende dallo specifico
altoparlante, ma in tendenza è omogeneo: cresce con l'escursione.
È facile osservare dai grafici, che hanno lo stesso andamento
generale per tutti gli altoparlanti, che con l'aumento dell'escursione:
Bl
diminuisce
Cms
diminuisce
Mms
aumenta
Res
diminuisce
Esaminando la struttura dei componenti di un altoparlante si può
osservare che con l'aumento dell'escursione:
- la bobina mobile esce dall'area
di maggior flusso magnetico, e questo giustifica la diminuzione
del Fattore di Forza
- la
sospensione si avvicina ai limiti meccanici, e questo giustifica la
diminuzione della cedevolezza; quando una molla è completamente
stirata la cedevolezza va a zero
- l'air
load, l'aria adiacente al diaframma che si muove in modo strettamente
solidale con il diaframma stesso, aumenta e questo giustifica l'aumento
della Massa mobile
- la diminuzione della Resistenza
elettrica equivalente alle perdite meccaniche significa che le perdite
meccaniche aumentano
La risultante di queste variazioni dei parametri è alla fine
riassunta dai grafici di Qms e
Qes, che in genere
aumentano con
l'escursione.
Conclusioni
Se avete il Sistema
Clio di Audiomatica e avete studiato accuratamente il manuale
sapete già quanto detto finora.
Clio automatizza in un unico strumento e programma (basta fare le
connessioni giuste sul pannello e impostare i parametri) le fasi di
“processing”, la rilevazione della risposta con segnale
sinusoidale, e “post-processing”, la conversione da
ampiezza a impedenza mediante calibrazione con un resistore di valore
noto e la stima dei Parametri.
Audiomatica suggerisce di effettuare le misure con segnale sinusoidale
e con il Metodo a tensione costante, spiegandone le ragioni.
Io non ho il Sistema Clio, e ho fatto questa serie di misure procedendo
con pazienza nel “post processing” dei dati prodotti da
Fuzz Measure; l'ho fatto anche perché sono dell'opinione che per
capire come stanno veramente le cose è necessario sbattere il
naso sui numeri grezzi e capire cosa c'è sotto i numeri prima di
utilizzare strumenti troppo sofisticati cioè totalmente
automatici.
Ho ripetuto le misure con i due sistemi e verificato i calcoli varie
volte, credo che il Metodo a tensione costante con segnale sinusoidale
vobulato dia risultati che sono generalmente validi in tutte le
condizioni e facilmente controllabili, d'altra parte i calcoli fatti
sui risultati di questa misura sono corrispondenti alla teoria standard
dei sistemi risonanti e danno parametri coerenti con gli sviluppi di
Clark e Klippel.
I parametri ottenuti con Speaker Workshop sono attendibili a basso
livello, ma non è noto come sia composto il segnale pseudo
casuale utilizzato, non sono disponibili risultati intermedi (un file
con frequenza e impedenza corrispondente), non so veramente che
algoritmo venga usato per il calcolo dei parametri, e infine alimentare
un altoparlante con una resistenza in serie di valore comunque elevato
e paragonabile o superiore alla Re sicuramente non riproduce le
condizioni normali di impiego di un altoparlante.
Potrebbe essere che l'utilizzo di Speaker Workshop non sia compatibile
con segnali ad alto livello, ma, stante che il segnale di ritorno
è attenuato esattamente quanto il segnale che alimenta
l'altoparlante è stato amplificato, per Speaker Workshop
è come se il “marchingegno” non ci fosse.
Si potrebbe anche osservare che la teoria di Thiele e Small è
valida per piccoli segnali e che i modelli semplificati da cui si
ricavano i parametri sono stati definiti appunto in queste condizioni.
Si può anche sostenere che l'elevata escursione porta
l'altoparlante a lavorare in zona non lineare e che l'elevata
distorsione può falsare il risultato delle misure.
Però anche l'analisi di R.H. Small per grandi segnali è
basata sugli stessi modelli, sapendo a priori che i modelli sono frutto
di approssimazioni, ma un modello approssimato è meglio di
nessun modello se si è consci delle approssimazioni introdotte.
E sia Clark che Klippel hanno sviluppato i sistemi di analisi del
comportamento per grandi segnali (a titolo di curiosità,
l'analisi eseguita nel Laboratorio Ciare sul PW252 è stata
eseguita con potenza variabile fino a 170 W nominali) senza modificare
il modello base, in quanto ad ampie escursioni un altoparlante resta
comunque un sistema risonante, sono solo diversi con l'escursione i
valori dei parametri.
Quello che manca non è un modello più accurato ma un
sistema di calcolo che introduca per ogni parametro uno o più
coefficienti che descrivano la variazione del parametro in funzione
dell'escursione.
E quando anche avessimo un simulatore siffatto, difficilmente potremmo
conciliare le dimensioni di un diffusore ottimizzato per bassi livelli
con le dimensioni di un diffusore ottimizzato per alti livelli.
Tanto più che non abbiamo ancora considerato le variazioni dei
parametri causate dalla temperatura della bobina mobile, per cui oltre
all'escursione dovremmo considerare anche la potenza media del segnale.
Non ci sono quindi conclusioni assolute che io mi senta di poter trarre
da queste misure, sono solo una serie di considerazioni spesso
contrastanti di cui bisogna comunque tener conto nella rilevazione e
soprattutto nell'utilizzo dei parametri, meglio: nella rilevazione dei
parametri tenendo conto dell'utilizzo dell'altoparlante.
Tento comunque di abbozzare alcune ipotesi.
Ipotesi 1
A basso livello il metodo a tensione costante e il metodo misto
sono più o meno equivalenti; per contro il metodo a corrente
costante e soprattutto il metodo a corrente costante semplificato non
sono a mio parere concettualmente attendibili.
La teoria dei Parametri TS è basata sul presupposto che il
livello del segnale sia basso; di fatto la teoria è valida al
100% solo per un altoparlante fermo.
Ipotesi 2
Non si può trascurare il comportamento di un altoparlante a livello di
segnale elevato.
Quando si ascolta musica in casa la potenza è comunque superiore
ai pochi milliwatt che si usano per misure a basso livello, e la
potenza dipende anche dal tipo di musica che si ascolta.
Quando si progetta un diffusore per uso diverso da HiFi domestico, ad
esempio una cassa per basso elettrico o per sintetizzatore o per
“organo elettronico” o una cassa PA si sa a priori che il
livello medio di segnale è molto elevato e il tipo di segnale
che alimenta il woofer può essere molto diverso dal segnale
musicale medio; ciò è tanto più vero in diffusori
dedicati a particolari strumenti musicali.
Tutte le case produttrici di altoparlanti utilizzano i Sistemi di
Klippel (forse nei paesi anglosassoni usano i Sistemi di Clark, ma
tant'è), e ciò significa che Clark e Klippel non hanno
sprecato 20 anni in elucubrazioni inutili.
Ipotesi 3
Quali Parametri debbo usare per un progetto?
Io, che non sono un fanatico dei 5 decimali dopo la virgola (3), credo
che per la progettazione di HiFi domestica i risultati di Speaker
Workshop siano più che sufficienti, e d'altra parte il rumore
pseudo casuale a larga banda di Speaker Workshop è
sicuramente più analogo ad un segnale musicale di una sinusoide
vobulata.
E sicuramente Speaker Workshop è estremamente comodo e rapido.
Quesito finale
A cosa servono i Parametri di TS se variano in misura così
consistente, oppure: quali sono i Parametri di TS “veri”?
A mio parere questa domanda può sorgere solo in chi si illude
che la realtà sia semplice e facilmente decifrabile, è in
cerca di certezze assolute e crede che per progettare un diffusore
basti avere un simulatore, inserire 6 numeretti (6 sono i
parametri necessari a BASS-PC per calcolare un allineamento, uno
ulteriore per calcolare la tenuta in potenza e uno che non viene
utilizzato) e schiacciare un pulsante.
Ringraziamenti
Ringrazio la Ciare e Mattia d'Antonio
per le misure con il Sistema Klippel sul PW252.
Note
1) per rinfrescare le idee su questa analogia Vi
rinvio ai miei articoli sulle Analogie
Dinamiche
2) la definizione
standard del fattore di merito è:
Q = 2π * (Energia immagazzinata nel circuito ) /
(Energia fornita dal generatore) che per alti fattori di merito
è equivalente alla formula indicata nel testo.
3) credo interessante rilevare che non molto tempo
fa Mauro Bigi e Maurizio Jacchia, i creatori del Sistema Clio, hanno
ricordato che la prima versione di Clio visualizzava i Parametri TS con
1 decimale.
Nelle versioni successive i decimali furono portati a 4 per rimediare
all'insoddisfazione di molti utenti che lamentavano la scarsa
precisione (sic) dello strumento.
È ovvio che tale "miglioramento" della precisione è stato
ottenuto semplicemente modificando la maschera di edizione dei numeri.
Immagino che quella modifica sia stata fatta passare come un
“miglioramento”, ed è giusto così, in quanto
è evidente che gli utenti che si lamentavano dell'imprecisione non
avevano in realtà la più pallida
idea di che cosa sia la precisione nelle misure, mentre gli utenti
esperti applicavano ipso facto l'arrotondamento come riflesso
condizionato.
È ben noto che nessuno ha mai guadagnato dimostrando al cliente che è
un cretino.
|
|
 |
|





























