Analogie Dinamiche

In tutti i simulatori per diffusori si usano modelli matematici per rappresentare le variabili fisiche in gioco: in questi modelli le grandezze fisiche appartenenti al regno della meccanica e dell'acustica, cioè la massa mobile del cono, l'aria contenuta nel box, la forza elastica della sospensione ecc. vengono “disinvoltamente” rappresentate con simboli che rappresentano grandezze elettriche, e vengono trattate con le tecniche matematiche tipiche dei circuiti elettrici.
Perché dico “disinvoltamente”? perché in genere nei manuali dei simulatori, nei quali questi modelli vengono presentati, si sorvola su una questione fondamentale: perché è lecito rappresentare l'aria contenuta in un box mediante un condensatore e l'aria contenuta in un condotto con una induttanza? perché sono differenti, se sempre di aria si tratta?
E poi, altrettanto importante: è questo l'unico modo di rappresentare queste grandezze?
Tutt'al più nella bibliografia si citano i soliti Beranek e Novak, e quando l'autore è in vena di modernismo Thomas e Rosa.
Ora, se questo può essere sufficiente in un manuale tecnico di un prodotto superprofessionale destinato a supertecnici, in quanto dovrebbe essere scontato che i suddetti supertecnici conoscano a menadito l'elettrodinamica, la meccanica e l'acustica (tutte e tre a fondo, e tutte le loro interazioni), oppure è lecito che in un articolo pubblicato sull'AES Journal nel 1970 si citi in bibliografia un testo del 1960, a mio parere ciò non è adeguato in manuali destinati a hobbisti o poco più (un prodotto venduto su internet a pochi euro è per definizione destinato ad utenti non professionali).

Il problema è tecnicamente conosciuto come problema delle “Analogie dinamiche”.

Analogie

come analizzare qualche cosa fingendo che sia qualche cosa d'altro

In ingegneria si parla di “Analogie” quando si descrive un sistema mediante modelli e metodi derivati da un sistema fisicamente diverso, da qui il sottotitolo.

E' ovvio che l'analogia deve essere giustificabile, cioè deve essere logicamente coerente, matematicamente  e fisicamente corretta e fornire risultati in accordo con il dato sperimentale.

L'obiettivo di queste note è di cercare di spiegare prima e giustificare poi le analogie, non tanto dal punto di vista puramente matematico ma dal punto di vista fisico, facendo ricorso più all'intuizione che alla matematica.
Quindi giungere a spiegare come funzionano i modelli usati nei simulatori e quale è il loro significato al di là del formalismo matematico.
Obiettivo molto ambizioso, debbo ammetterlo; è mia convinzione che per usare bene un simulatore si debbano avere ben chiari i principi fisici su cui è basato e soprattutto i limiti dei modelli utilizzati.
Altrimenti, soprattutto nel caso dei simulatori di diffusori, c'è il rischio di aver buttato sia i soldi del simulatore (pochi) che i soldi dei componenti (molti), senza rendersi conto che ciò che esce dal simulatore è solo il punto di partenza, non il punto di arrivo del progetto.

1.    Perché le analogie si usano e sono necessarie?

Fondamentalmente le analogie si usano per due ragioni:

•  per un sistema è stato sviluppato un formalismo più efficace e più approfondito, soprattutto dal punto di vista dei metodi applicativi, che per un altro
• un sistema è misto, cioè composto da componenti di natura diversa, e per descriverne il comportamento complessivo si deve unificare il modello, costruire un modello complessivo che rappresenti grandezze di natura diversa 

Il diffusore acustico è un sistema complesso elettrico-meccanico-acustico, che riceve un segnale elettrico, lo trasforma in forze meccaniche che vengono a loro volta trasformate in pressione acustica.


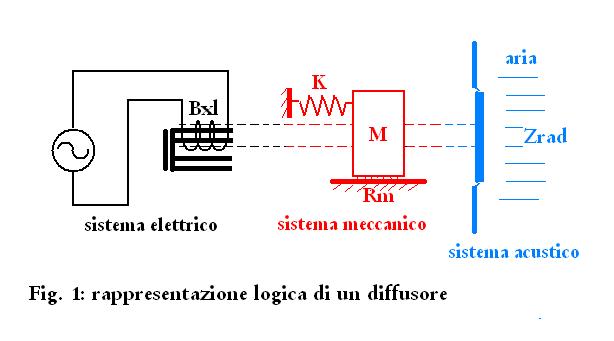
Nel diffusore diversi elementi elettrici, meccanici ed acustici coesistono e soprattutto si influenzano a vicenda, e si vuole essere in grado di capire (cioè predire):

• la pressione acustica generata in funzione del segnale elettrico (la curva di risposta)
• la reazione del diffusore al segnale (l'impedenza elettrica risultante)
• i limiti di utilizzo (l'escursione del cono).

Quello che si vede in Fig. 1 non è un modello utilizzabile tecnicamente, è solo una rappresentazione intuitiva della trasformazione di energia da una forma ad un'altra.
Quando si parla di “modello” si intende un sistema di grandezze quantificate e le cui leggi di funzionamento siano ben definite, un modello serve a fare calcoli e previsioni quantificate.
I modelli usati in questo campo sono modelli “a costanti concentrate”  per non avere un modello comunque troppo complesso per essere trattato, e ciò implica alcune assunzioni e molte semplificazioni che ne limitano la validità ad un ambito ristretto e ben definito.
Un modello a costanti distribuite che comprendesse grandezze elettriche, meccaniche ed acustiche credo sarebbe un oggetto mostruoso, se mai fosse possibile costruirlo; comunque qualsiasi modello, per lo stesso fatto di essere un modello, richiede semplificazioni ed approssimazioni,
Il “riduzionismo” conseguente non è gratis, quindi capire bene cosa sta “sotto” un modello semplice, come quelli che vengono comunemente usati nei sistemi di simulazione, è importante sia per capire come funziona sia per capire fino a dove funziona.

2.    Un po' di basi

Partiamo dall'analizzare gli elementi semplici che costituiscono un diffusore, per riassumerne i principi di funzionamento e focalizzare l'attenzione su tutto ciò che attiene alla modellizzazione; passeremo poi ad analizzare le “analogie” possibili dei costituenti elementari, per capire poi come utilizzarli per modellare i sistemi.

L'altoparlante

Cominciamo da un breve riepilogo sull'altoparlante: già visto mille volte, tanto per fissare i termini.

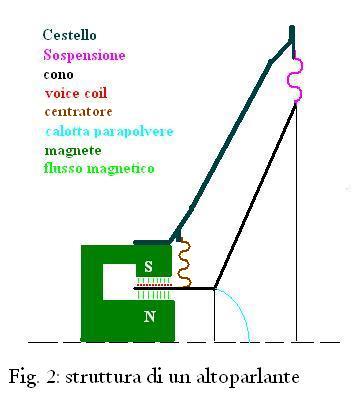L'altoparlante è un sistema elettromeccanico, composto da una parte elettromagnetica: magnete e voice coil, e da una parte meccanica: cono, supporto della voice coil, sospensione e centratore.
Tralascio il cestello perché non ha alcuna funzione se non quella di tenere assieme il tutto.

La voice coil ed il magnete costituiscono il “motore” del sistema, quella parte che trasforma il segnale elettrico (la corrente alternata che proviene dall'amplificatore) in un movimento meccanico.

Il cono, che è rigidamente (idealmente) collegato alla voice coil, funziona da pistone per trasmettere il movimento meccanico all'aria.

Il cono: un sistema meccanico oscillante

La parte meccanica mobile dell'altoparlante ha una caratteristica: ha una massa, costituita dalla massa del cono, della voice coil (che è in rame o alluminio) e del suo supporto (cartone, fibra sintetica, alluminio), dalla massa del centratore e della sospensione.

Questa massa, che possiamo in prima approssimazione considerare un corpo unico rigido, è collegata all'ambiente (cioè al cestello) da una forza elastica, la sospensione (in questa astrazione abbiamo separato la sospensione nei suoi due componenti, la massa e la forza elastica, come se fossero due parti separate).

L'altoparlante è quindi un sistema risonante:  in Fig 3a abbiamo il modello semplificato di un sistema massa-molla a riposo.

A rappresenta il fatto che la molla è fissata ad una estremità in modo rigido, M è la massa connessa in modo rigido all'altra estremità della molla, la molla ha la propria costante elastica K, che la caratterizza completamente, definita in questo modo:

F  =   - K * x                         1.1        (legge di Hooke)

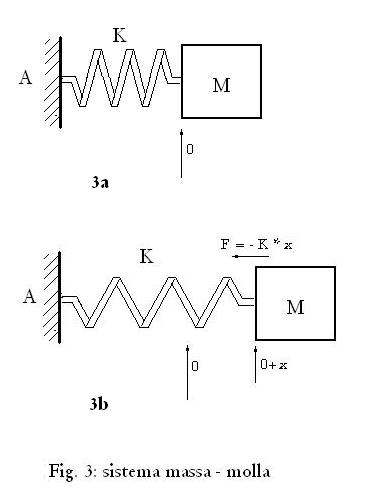
dove x è l'allungamento della molla, cioè lo spostamento dalla posizione di riposo, quando viene sottoposta ad una forza F; in altre parole una molla con costante elastica K esercita una forza F proporzionale all'allungamento x.

Il segno – tiene conto del fatto che la forza esercitata dalla molla è in verso contrario allo spostamento e quindi tende a riportare la molla in posizione di riposo.

La Fig. 3b illustra il sistema massa – molla quando viene spostato dalla posizione di riposo (applicando alla massa una forza -F).

Supponiamo ora un sistema ideale massa – molla:

ideale significa che:

la massa non è sottoposta a nessuna forza tranne quella della molla

la molla è collegata ad un “ambiente” A assolutamente rigido (cioè che non subisca alcuno spostamento quando soggetto ad una forza)

non c'è alcun tipo di dissipazione, quindi la massa si muova senza attrito

la molla è perfetta, cioè l'unica legge che governa il suo funzionamento è la 1.1, ed è priva di massa.

In Fig. 4 vediamo l'evoluzione degli stati del sistema massa – molla, vediamo cioè che cosa succede quando la massa viene spostata dalla posizione di riposo, dal momento in cui essa (la massa) viene rilasciata.

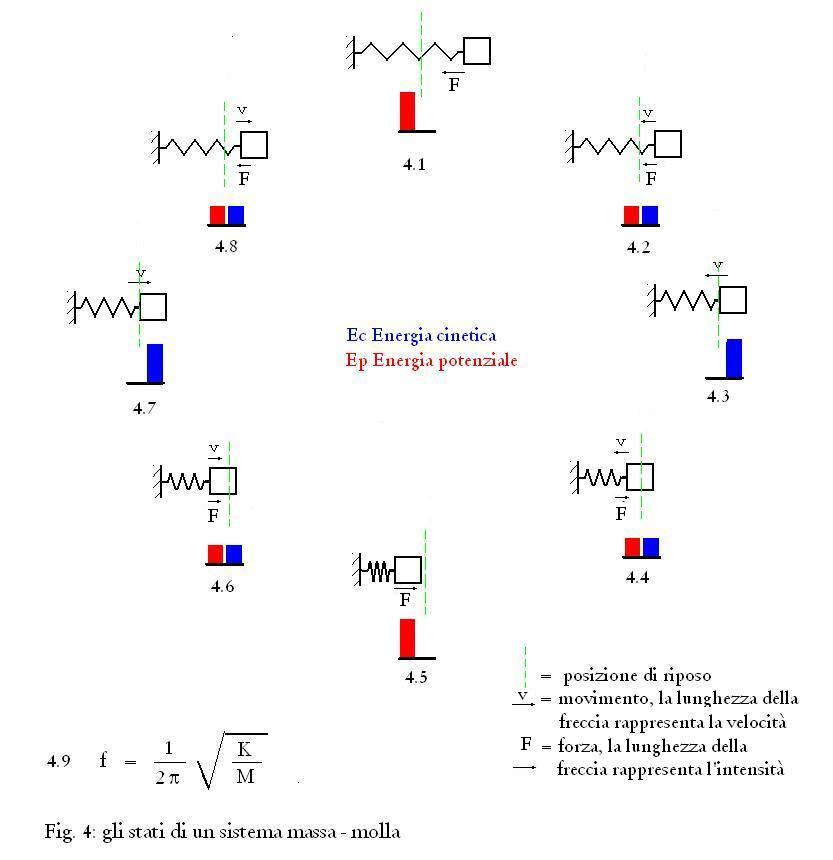
In Fig. 4.1 la massa viene spostata dalla posizione di riposo da una forza applicata, e quindi viene liberata; la molla si è caricata e quando viene liberata, la forza elastica della molla tende a riportare la massa alla posizione di riposo.

In questo movimento la massa acquista velocità, mentre la molla si scarica (Fig. 4.2).

In Fig. 4.3 la massa nel suo movimento giunge alla posizione di riposo; in questa posizione la forza si annulla (in base alla 1.1) e la massa in movimento ha raggiunto la sua massima velocità; la massa non può fermarsi istantaneamente ma prosegue, a causa della sua inerzia.

Da questo punto la molla agisce in senso inverso, la forza elastica è in verso opposto al moto e quindi rallenta la massa fino a fermarla nella posizione di massima elongazione della molla in verso opposto (Fig. 4.5).

Da questo momento il processo si ripete (forza e spostamento sono opposti alla prima parte del ciclo) e quindi la massa viene riportata alla posizione di riposo (Fig. 4.7), e così via.

Si genera un movimento oscillatorio regolare la cui frequenza dipende dalla massa e dalla forza elastica della molla: maggiore è la massa e più bassa è la frequenza, più forte è la molla più alta è la frequenza.
E' facilissimo fare un esperimento: prendete un elastico (abbastanza lungo per vedere meglio l'effetto) ed appendetevi un peso qualsiasi (sufficiente ad allungare di circa un terzo l'elastico, solo per rendere l'effetto visibile), un mestolo da cucina oppure una pinza da meccanico vanno benissimo, quindi tiratelo verso il basso (non troppo) e lasciatelo andare.
Poi aggiungete un altro peso, un altro mestolo o un'altra pinza e ripetete l'esperimento: l'oscillazione è più lenta.
Poi potete ricominciare con due elastici (i due elastici in parallelo, non in serie – la ragione di questa precisazione, che è ovvia, sarà chiara in seguito), per sperimentare con una molla più forte.

La chiave di tutto: l'energia

Che cosa succede nel sistema oscillante?
La chiave per capire il fenomeno è l'energia, nelle sue varie forme, ed il Principio di conservazione dell'Energia.
Succede che il sistema oscillante a riposo ha energia propria nulla; quando si applica una forza per spostare la massa la molla si carica di energia, che è energia statica, energia potenziale  Ep, capacità di compiere un lavoro quando siano tolti i vincoli.

Quando si rilascia la massa questa capacità di compiere un lavoro ha effettivamente la possibilità di compierlo e muove la massa per riportarla alla posizione di riposo, la massa in movimento acquista energia di movimento, energia cinetica Ec, mentre la molla si scarica e quindi l'energia potenziale diminuisce (da fig 4.1 a 4.3).

Quando la massa arriva alla posizione di riposo (Fig. 4.3) l'allungamento  della molla è uguale a zero quindi l'energia potenziale è nulla, ma la massa ha acquistato velocità e quindi energia cinetica: in questa posizione la molla è in posizione di riposo quindi non comunica più alcuna forza alla massa, che quindi non aumenta più la propria velocità (l'accelerazione è nulla, a=F/M), da questo punto in avanti la molla si oppone al movimento, rallentando la massa e caricandosi di energia potenziale (Fig. 4.5).

Un principio fondamentale della fisica dice che l'energia totale di un sistema chiuso (cioè isolato) è costante: nel nostro caso ideale (mancanza di attriti) si ha una trasformazione fra energia potenziale ed energia cinetica, tale che la somma delle due forme di energia è costante.
Nel movimento oscillatorio perfetto si dimostra che il sistema, una volta eccitato, oscilla con ampiezza costante, con un moto detto armonico, ad una frequenza costante definita dalla equazione di Fig. 4.9.

Il movimento del cono nel moto armonico

Nel moto armonico, fra le grandezze fondamentali del movimento:

• spostamento dalla posizione di riposo
• velocità
• accelerazione (che è proporzionale alla forza che agisce sulla massa in movimento:  F  =  M*a)

sussistono le relazioni di Fig. 5, dove i numeri sull'asse orizzontale corrispondono agli stati di Fig. 4.

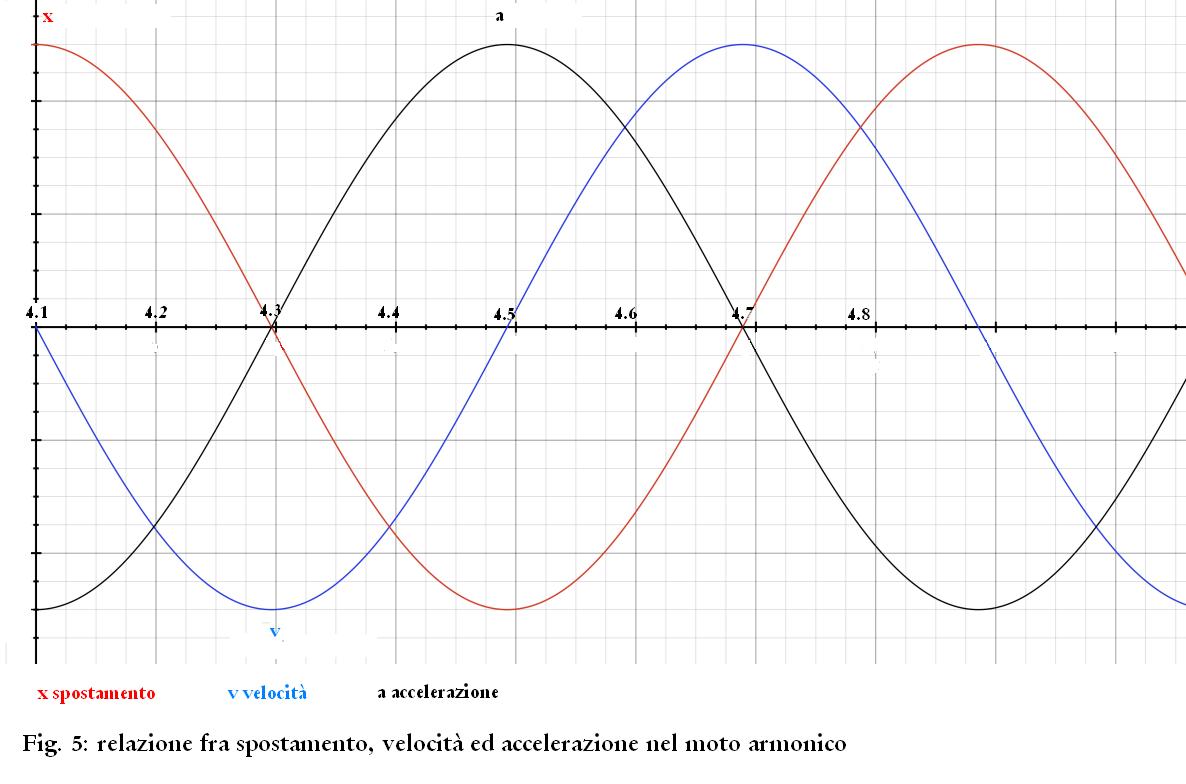
Detta  A  l'ampiezza del moto, si dimostra che (pi  è il p greco) :

in 4.1        x  =   A
                 v  =   0
                 a  =   - A * 2pi * f               

in 4.3        x  =   0
                 v  =  - A * 2pi * f                    2.1
                 a  =  0

in 4.5        x  =  - A
                 v  =  0
                 a  =  A * 2pi * f

che ci dicono che quando l'ampiezza dello spostamento è massima l'accelerazione è massima in verso opposto (la molla manifesta la sua azione  secondo la  1.1) e la velocità è nulla (la massa inverte il suo moto quindi per un istante è ferma), mentre quando la massa passa per la posizione di riposo (spostamento = 0) la velocità è massima e l'accelerazione è nulla (la molla passa per la posizione di riposo quindi non esercita alcuna forza).
La forma dell'equazione della velocità, che dipende direttamente dalla frequenza del moto, è molto importante e deve essere tenuta a mente per i prossimi sviluppi.
In base alla II legge di Newton la forza esercitata dalla molla è proporzionale alla accelerazione ed in fase con essa.
Il moto armonico smorzato

Quanto detto fino ad ora vale nel caso di sistema senza attriti, cioè senza forze dissipative.

Che cosa succede quando il sistema non è ideale, cioè quando ci sono attriti?

Il principio di conservazione dell'energia è ancora valido, ma in questo caso gli attriti trasformano ad ogni ciclo una parte dell'energia disponibile in energia termica, che viene dispersa nell'ambiente e non è più recuperabile per compiere lavoro utile.
Pertanto ad ogni ciclo una piccola porzione dell'energia cinetica (e potenziale) viene persa, l'energia totale dovuta al movimento o alla posizione diminuisce ed l'oscillazione di conseguenza diminuisce di ampiezza, fino a cessare del tutto, quando tutta l'energia iniziale è stata trasformata in calore.

La forza dissipativa ha le origini più varie, può essere dovuta allo strisciamento superficiale di due parti meccaniche, al movimento in un fluido viscoso, ad una deformazione non perfettamente elastica: in una molla reale la deformazione causa microattriti interni nel materiale di cui la molla è costituita; la stessa cosa succede quando un materiale come ad esempio il legno viene sottoposto a vibrazioni.
L'attrito è un fenomeno decisamente complesso, e per descriverlo in modo ragionevolmente semplice si debbono fare semplificazioni notevoli.
In genere si assume che per un corpo, in movimento sufficientemente lento, la forza dissipativa è pari a:

F  =  -  Rm *  v                 2.2

dove Rm è detta Resistenza meccanica    e    v    è la velocità di spostamento.
Il segno  -  tiene conto che la forza dissipativa è in verso opposto al verso del movimento.

Il moto armonico smorzato forzato

Per mantenere costante l'oscillazione del nostro sistema molla – massa in presenza di forze dissipative è necessario fornire in altro modo al sistema l'energia dissipata sotto forma di calore dagli attriti.

L'energia dissipata vale:

Ed       =       Rm * v ^2                2.3

Dobbiamo quindi agire sulla massa M con una forza che sia contraria alla forza dissipativa: dato che stiamo parlando di movimento oscillatorio anche la forza applicata esternamente deve essere concorde con la forza della molla, quindi deve essere una forza oscillante, che rappresentiamo come in Fig 6.

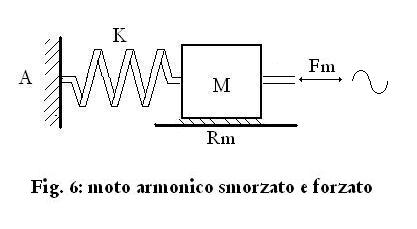
Che cosa succede se applichiamo una forza oscillante la cui frequenza non coincide con la frequenza di risonanza? 

Quando la frequenza della forza Fm coincide con la frequenza di risonanza del sistema massa – molla,  l'azione della molla e della forza esterna si sommano e il moto oscillatorio raggiunge la sua massima ampiezza.

Quando la frequenza della forza Fm non coincide con la frequenza di risonanza del sistema le azioni delle due forze non si sommano più ad ogni istante, bensì in qualche istante si sommano ed in qualche altro istante si contrastano, quindi il moto oscillatorio diminuisce di ampiezza e viene tenuto attivo solo dalla forza esterna Fm.

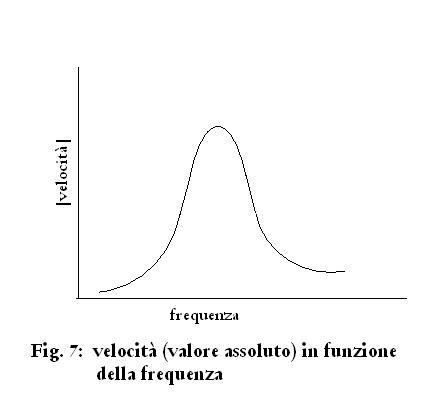
La velocità di movimento della massa M si comporta come in Fig. 7  (vedremo in seguito perché focalizzo l'attenzione sulla velocità).

L'ambiente: l'aria

L'altoparlante suona perché è immerso nell'aria, che è un fluido comprimibile.
L'aria è un gas, quindi composto da particelle (ossigeno, azoto e altre molecole di natura varia in percentuale minore ma oggigiorno crescente, pulviscolo ecc) in continuo movimento casuale: le particelle occupano una parte minima dello spazio disponibile, e si muovono urtandosi fra loro e rimbalzando ed urtando le pareti dell'ambiente in cui si trovano, venendo respinte da esse, come le palle su un tavolo da biliardo, come in Fig. 8.

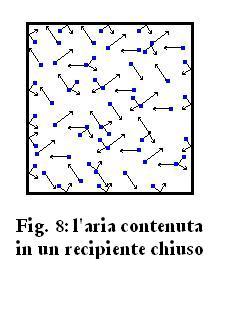
Essendo composta da particelle l'aria ha una densità  ro, cioè una massa per unità di volume, che in condizioni standard è pari a 1,18 Kg / m3.

Essendo le particelle in movimento casuale, si urtano fra loro ed urtano le pareti del recipiente che le contiene; questi urti comunicano una forza alle pareti stesse: si dice che il gas ha una pressione  P, una forza per unità di superficie, cioè l'aria esercita una forza sui corpi immersi in essa e sulle pareti dell'ambiente in cui è contenuta; la pressione normale dell'aria in cui viviamo è pari a circa 1 Kg / cm2.

La pressione è dovuta all'energia termica contenuta nell'aria: è l'energia termica che tiene in movimento le particelle (ovvero: l'energia è il movimento delle particelle).
In condizioni statiche il movimento netto delle particelle è nullo, per ogni particella che si muove in una direzione un'altra si muove in direzione opposta, poi le particelle si urtano e rimbalzano cambiando direzione: dal punto di vista macroscopico l'aria è ferma e statisticamente le particelle sono in equilibrio.

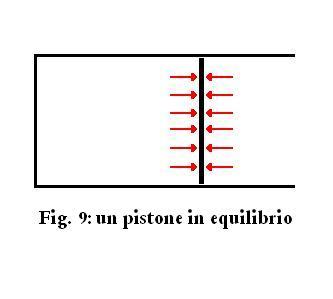
Supponiamo che l'ambiente che contiene l'aria abbia una parete mobile, un pistone come in Fig. 9: essendo il sistema immerso nell'aria esterna la pressione esterna equilibra quella interna, la forza esercitata dalla pressione dell'aria sulla parete interna del pistone eguaglia la forza esercitata dall'aria esterna sulla parete esterna del pistone ed il pistone è fermo.

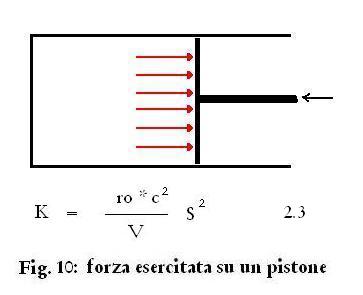
Se si esercita una forza aggiuntiva sul pistone, come in Fig. 10, il pistone si sposta, il volume interno diminuisce quindi la pressione aumenta fino a che la forza generata dalla pressione interna eguaglia la forza generata dalla pressione dell'aria esterna più la forza aggiuntiva (i sistemi fisici tendono sempre all'equilibrio).

L'aria contenuta nella cavità si comporta come una molla (per piccoli spostamenti del pistone), come ci dice la 2.3   che definisce la Costante elastica dell'aria contenuta nella cavità, dove V è il volume della cavità, S la superficie del pistone, ro la densità dell'aria e c la velocità del suono.

Prima divagazione

Facciamo ora un piccolo esercizio sul sistema di Fig. 9 e 10.

In un gas perfetto vale la legge:

P * V  =  costante * T                    2.4

dove T è la temperatura del gas e la costante dipende in linea di massima dalla densità del gas.
Questo vale anche per il gas contenuto nel sistema di Fig. 9 e 10, il gas ha pressione P, il volume della cavità è V, la superficie del pistone è S, il pistone si muove senza attrito e senza trafilamento d'aria (e cominciamo a semplificare).
Cosa succede se spingiamo il pistone, variando il volume V di una quantità   dV?
Dato che siamo in vena di semplificazioni, diciamo che se spostiamo di poco il pistone la temperatura T non varia in modo significativo, diciamo anzi che non varia proprio.
D'altra parte nel sistema a riposo la pressione esterna e quella interna sono uguali, se spostiamo il pistone la pressione interna varia e si assume che quella esterna rimanga costante, quello che è rilevante quindi è la variazione di pressione, che chiamiamo   dP.

Dato che P * V = costante possiamo scrivere:

P * V  =    ( P + dP ) * ( V + dV )            2.5

Con due banali passaggi arriviamo a:

P *  dV   =  V * dP  -  dP * dV            2.6

Dato che abbiamo assunto che dV sia piccolo, anche dP sarà piccolo quindi il termine dV * dP è trascurabile, da cui:

dP  =   P   *   dV /  V                2.7

ma la pressione è una forza su una superficie, quindi  la  2.7  ci permette di calcolare la forza necessaria per spostare il pistone di una distanza qualsiasi (purché piccola).

Mettiamoci un po' di numeri:

Diciamo che V è 91 litri, il diametro del pistone è 26 cm e lo spostamento è 3 mm (questi numeri non sono affatto casuali).

Il diametro di 26 cm corrisponde ad una superficie di 530 cm2, quindi lo spostamento di 3 mm corrisponde ad una variazione di volume di 159 cm3, che rispetto al volume di 91 litri equivale a  0,00175 * V: possiamo sicuramente considerare piccolo lo spostamento e quindi le semplificazioni fatte sono accettabili.

In base alla  2.7,  dP vale circa  0,00175 Kg / cm2 che, su una superficie di 530 cm2 dà una forza pari a circa 0,92 Kg.

Prima considerazione:  la variazione di volume risulta inferiore allo  0,2 %  pertanto la non linearità introdotta dalla forma iperbolica della 2.4 è del tutto trascurabile.

Quindi la forza sviluppata dal gas è con ottima approssimazione lineare e corrispondente alla legge   F  =  - K * x.

Seconda considerazione: i numeri utilizzati nell'esempio non sono casuali, corrispondono ad alcuni parametri meccanici del woofer Ciare  PW328, quella descritta nell'esempio è la definizione del Vas, che nel PW328 è appunto 91 litri; il Vas è la definizione della costante elastica delle sospensioni dell'altoparlante (il Vas si definisce come il volume di aria che ha una cedevolezza uguale alla cedevolezza delle sospensioni, per una superficie pari alla superficie proiettata del cono; ricordo che la cedevolezza è semplicemente l'inverso della costante elastica).

Seconda divagazione

Ora che abbiamo capito che l'aria contenuta in una cavità si comporta (con alcune approssimazioni) come una molla, consideriamo il sistema di figura 11.





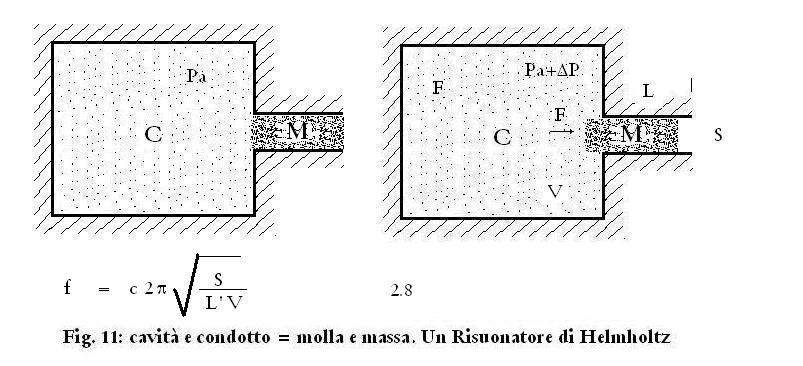
Abbiamo una cavità C di volume V  con un condotto di superficie S e lunghezza L che comunica con l'esterno.
L'aria contenuta nel condotto ha una sua massa  M  =   (Volume del condotto) * (densità dell'aria), che risente dell'azione elastica dell'aria contenuta nella cavità: quindi anche qui abbiamo un sistema molla – massa, che ha pertanto una sua frequenza di risonanza: questo è esattamente un Risuonatore di Helmholtz.

La frequenza di risonanza dipende:

1. dal volume del condotto (che determina la massa dell'aria oscillante), quindi dalla sua superficie e lunghezza
2. dal volume della cavità, che determina la costante elastica dell'aria contenuta nella cavità (in base alla 2.3 e alla 2.7.), ovviamente fissate le condizioni operative, cioè pressione atmosferica e temperatura.

Per calcolare il sistema meccanico massa – molla avevamo fatto alcune assunzioni sul sistema massa – molla,  che deve essere ideale.

Quali sono le approssimazioni che accettiamo per impostare un calcolo sul Risuonatore di Helmholtz?
Considerare il sistema cavità – condotto come un sistema massa – molla ideale significa adottare un modello “a costanti concentrate”, in cui:

l'aria contenuta nel condotto si muove come un corpo rigido e senza attriti:
qui l'approssimazione è veramente rilevante

• l'aria lungo le pareti del condotto, a causa della viscosità, non si muove alla velocità dell'aria contenuta nel centro del condotto. Pertanto il condotto deve avere una sezione abbastanza grande da permetterci di trascurare l'effetto superficie del condotto e comunque una forma non “estrema”, in quanto una “tagliatella” di 1 x 200 cm, pur avendo una superficie totale di 200 cm2 in pratica ha solo effetto superficie

• la pressione deve essere uniforme lungo il condotto (corpo rigido significa non comprimibile) quindi il condotto deve essere abbastanza corto da poter trascurare le differenze di pressione lungo il condotto

• l'aria alle due estremità del condotto appartiene  al condotto,  ed appartiene anche  sia alla cavità (ad una estremità)  che all'ambiente esterno (all'altra), inoltre il suo comportamento dipende da come sono realizzati i bordi del condotto (a spigolo vivo, smussati con profilo circolare piuttosto che iperbolico o esponenziale ecc), quindi definire il volume del condotto non è semplice. Una approssimazione che per forme del condotto regolari risulta sperimentalmente abbastanza valida è che la lunghezza del condotto viene aumentata di una quantità pari a    0,85 * (diametro del condotto) : per questo motivo nella 2.8 compare L' al posto di L.

non si considera la massa dell'aria contenuta nella cavità
anche questa approssimazione è significativa:

• mentre nel caso di un sistema meccanico è ragionevole che la massa della molla sia trascurabile rispetto alla massa oscillante, in questo caso la massa d'aria contenuta nella cavità è molto maggiore della massa dell'aria del condotto, e può essere trascurata solo se la pressione è uniforme all'interno della cavità: in altre parole la lunghezza d'onda deve essere molto maggiore di tutte le dimensioni della cavità.
• La cavità deve quindi avere una forma “regolare”, il calcolo per una canna d'organo è diverso.

la forza elastica dell'aria nella cavità è lineare
ciò è vero solo per ampiezza dell'oscillazione ridotta, questo è per altro richiesto anche per poter considerare l'aria nel condotto come un corpo rigido.

Le pareti della cavità sono assolutamente rigide
ciò significa che non si muovono sotto l'azione della forza elastica dell'aria contenuta; nel caso di pareti reali di materiale reale il movimento delle pareti implica dissipazione dell'energia comunicata dalla forza elastica.

Come si vede le approssimazioni che siamo costretti ad introdurre per poter costruire un modello ragionevolmente semplice del sistema meccanico – acustico sono molto più significative che nel modello puramente meccanico: è entrata in gioco anche la lunghezza d'onda, e questa è una approssimazione che influisce pesantemente in tutti i sistemi acustici.
E' chiaro che stiamo parlando di modelli “a costanti concentrate”, che sono applicabili solo quando la distribuzione dell'energia è uniforme, cioè quando le dimensioni fisiche del sistema (nel nostro caso tutte le dimensioni, sia della cavità che del condotto) sono molto minori della lunghezza d'onda del suono che viene trattato.

Il suono

In un diffusore acustico Il suono si genera perché lo spostamento del cono generato dalla corrente che scorre nella voice coil rompe l'equilibrio fra pressione interna e pressione esterna (o, generalizzando, fra la faccia anteriore e quella posteriore), comunicando una spinta in una direzione precisa alle particelle che urtano la superficie del cono, le quali a loro volta comunicano questa spinta alle particelle contro cui rimbalzano, e così via: si ha pertanto un aumento locale di pressione in quanto viene aggiunta energia cinetica alle particelle di gas colpite dal movimento del cono.
Dato che le particelle sono molto piccole e mediamente molto lontane fra loro la trasmissione del moto fra le particelle non è istantanea, l'onda di pressione che viene trasmessa all'ambiente circostante si sposta con una velocità finita, che dipende dalla densità dell'aria (in prima approssimazione).

Ovviamente l'aria si oppone al movimento del cono (principio di azione e reazione).

Il cono si muove di moto alternato, quindi si ha una successione di compressione e rarefazione che si propaga nell'ambiente, come in Fig. 12.

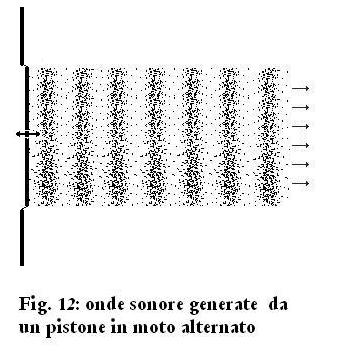Nella figura 12 abbiamo fatto una ulteriore approssimazione: il cono si comporta come un pistone piatto.
Ma ciò è vero solo quando le dimensioni del cono sono trascurabili rispetto alla lunghezza d'onda; in effetti quando nella letteratura tecnica si parla di “superficie del cono” si intende sempre “superficie proiettata”, come se al posto del cono ci fosse un pistone piatto.

Il livello del suono prodotto dipende quindi dalla pressione, e più esattamente dalla pressione “aggiunta” alla pressione atmosferica dal movimento del cono; quando parliamo di “pressione acustica” o genericamente di pressione intendiamo la differenza di pressione rispetto alla pressione atmosferica, che indicheremo con Pa.
La pressione è determinata dal movimento caotico delle molecole di aria, più il movimento è veloce maggiore è la pressione, la quale in sostanza è causata dall'energia cinetica delle molecole, pertanto dalla velocità.

In base al meccanismo spiegato sopra è evidente che la pressione acustica dipende dalla velocità di spostamento del cono, essendo sostanzialmente un trasferimento di energia cinetica: più il cono si muove velocemente più energia cinetica trasferisce all'aria.
Questo dà ragione del fatto che per ottenere una pressione costante al variare della frequenza, l'ampiezza dello spostamento deve essere inversamente proporzionale alla frequenza (in base alla 2.1).

come la matematica ci aiuta a trasformare le mele in pere

Finora abbiamo esaminato alcuni elementi costitutivi degli altoparlanti, focalizzando l'attenzione sulla parte meccanica della faccenda: anche quando abbiamo parlato di acustica, in realtà abbiamo privilegiato l'aspetto meccanico del fenomeno.
E' vero che l'aspetto meccanico e quello acustico della trasmissione del suono nell'aria sono strettamente legati, ma gli oggetti fisici sono corpi rigidi (nel senso che non sono comprimibili) che nelle approssimazioni fatte non hanno dimensioni, mentre l'aria, che è un gas, non è un corpo rigido (nel senso che è comprimibile) e le dimensioni del sistema acustico non si possono trascurare ma bisogna tenerne conto nelle approssimazioni.
Abbiamo anche visto quante approssimazioni sono state necessarie per trattare analiticamente (cioè matematicamente) i fenomeni: se nel campo della meccanica le approssimazioni sono tutto sommato abbastanza ovvie e non “eccessive”, quando si arriva a trattare i fenomeni meccanici nei gas le approssimazioni sono veramente importanti, tanto da imporre pesanti limiti all'applicabilità dei modelli matematici.

Ma l'obiettivo primario è non solo trovare un modello matematico, cioè le equazioni che descrivono il funzionamento del sistema, unificato fra meccanica ed acustica, ma soprattutto trovare un modello matematico che ci permetta di trattare tutti i fenomeni:  meccanici, acustici ed elettrici,  in un modo unico, con le tecniche che conosciamo meglio e che quindi siamo in grado di trattare con maggiore disinvoltura: dobbiamo trattare (dal punto di vista del calcolo) tutta la realtà come se fosse un circuito elettrico.

Dato che si tratta di progettazione è giocoforza introdurre un po' di matematica in più, ma anche in questa puntata non esporrò dimostrazioni e derivazioni analitiche delle soluzioni di equazioni: queste si possono trovare in qualsiasi testo; quello che mi preme è giungere ad una comprensione intuitiva di ciò che sta “sotto” la matematica.
So che è un obiettivo ambizioso e decisamente difficile.
E' anche importante capire che spesso sotto la matematica non c'è null'altro che matematica, ma con quest'artificio siamo in grado di fare calcoli che funzionano; capire questo è forse ancora più difficile.

La dissipazione dell'energia

Cerchiamo di arrivare per gradi a capire come si può arrivare ad una trattazione unificata di cose così diverse, quindi partiamo dal caso più semplice: i fenomeni dissipativi.

Resistenza meccanica

In Fig. 6 abbiamo visto una forza dissipativa meccanica, con le due equazioni fondamentali: la 2.2 che tratta della Forza, e la 2.3 che tratta dell'energia dissipata, in funzione della Resistenza meccanica (che è la caratteristica dell'attrito) e della velocità del corpo.

Nella 2.2 possiamo trascurare il segno, in quanto vogliamo considerare la Forza che è necessario applicare al corpo di massa M per mantenerlo in moto a velocità costante v, e questa forza,  per il III principio della dinamica (azione e reazione) è uguale (in valore assoluto) e contraria (nel verso) alla forza generata dall'attrito.

La 2.2 diviene quindi (in un banale passaggio matematico):

Rm  =    F /  v                    2.2'

Resistenza elettrica

C'è una totale somiglianza con la legge di Ohm:

Re  =    V  /  i                    3.1

anche la 2.3 ha una totale somiglianza formale con l'equazione dell'energia dissipata da una resistenza:

Ed   =    Re  *   i2                 3.2

se identifichiamo la forza F con la tensione V  e  la velocità  v  con la corrente i.

Questa identificazione è ragionevole, oltre che formalmente valida?

Da un punto di vista fisico la forza indica la capacità di compiere un Lavoro, che si concretizza quando la forza viene applicata ad un corpo e lo muove: il corpo quindi acquista velocità, cioè energia cinetica.
La tensione elettrica viene detta anche “potenziale elettrico” in quanto indica la capacità di compiere un lavoro, che si concretizza quando viene applicata ad un dispositivo ed in questo dispositivo scorre corrente: è la corrente che crea calore (energia termica) o  muove il cono dell'altoparlante (energia cinetica), non la tensione.

Quindi l'analogia  Forza – Voltaggio appare ragionevole.

La corrente ci dice quanti elettroni attraversano il dispositivo nell'unità di tempo: si parla pertanto di “Flusso”.

La velocità di un corpo ci dice (è una definizione un po' grossolana, ma sostanzialmente corretta) quanta materia attraversa lo spazio nell'unità di tempo: anche per la velocità si può quindi ragionare in termini di “Flusso”.

Anche l'analogia velocità – corrente è quindi ragionevole.

Resistenza acustica

Nel campo dell'acustica ha senso un concetto di Resistenza acustica?
Qui il ragionamento deve essere più articolato.

Se partiamo dalla dinamica dei fluidi (cioè il comportamento di un gas in movimento) vediamo facilmente che, per comprenderne il funzionamento, dobbiamo passare dal concetto di Forza a quello di Pressione, che non è altro che una Forza per unità di Superficie.

E' esperienza comune che si soffia meglio in un tubo corto e di sezione grande che in un tubo lungo e sottile: nel primo passa più aria per unità di tempo rispetto al secondo, a parità di pressione.

Ciò che caratterizza il moto del gas è la quantità di gas che attraversa una superficie (che può essere una sezione del condotto del Risuonatore di Helmholtz di Fig. 11 oppure una superficie ideale parallela al pistone di Fig. 12)  nell'unità di tempo: anche qui vale il concetto di “Flusso”.

Il caso generico dell'aria contenuta in un tubo è rappresentato in Fig. 13
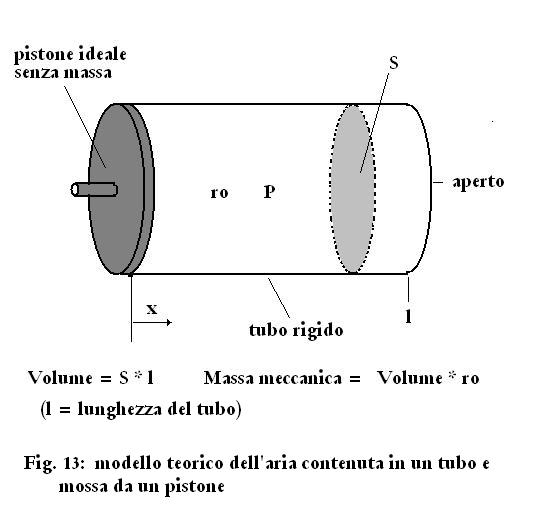La quantità di gas, ad esempio contenuta nel condotto del risuonatore, è definita dal suo volume, quindi dalla superficie per la lunghezza del condotto.

Ciò che caratterizza un flusso di gas è detto “velocità di volume”, che identifica il volume di gas che attraversa una superficie nell'unità di tempo: parliamo di volume geometrico, il volume di gas moltiplicato per la densità del gas ci riporta alla massa di gas, e si torna al concetto meccanico di massa.

Diamo le seguenti definizioni:

u  =    S  *  v                    3.3

dove    u  è la “velocità di volume”,  S  è la superficie della sezione attraversata dal gas,  v  è la velocità media delle molecole di gas.

Nel caso del suono non abbiamo un flusso costante di gas, ma un flusso alternato, in quanto il suono è costituito da onde di pressione, quindi da addensamenti e rarefazioni del gas.
Per creare questi addensamenti e rarefazioni le molecole compiono un percorso che nel gas a pressione “normale” è molto maggiore del percorso che le molecole compiono quando si urtano reciprocamente nel loro moto termico: teniamo conto che la lunghezza d'onda del suono è molto grande rispetto alla distanza fra le molecole ed inoltre l'escursione di un cono si misura in millimetri, non in milionesimi di millimetro.

Quindi anche nel caso del suono ha senso parlare di velocità di volume e di flusso: semplicemente sono alternati anziché continui.
Ciò che il suono trasmette all'ambiente in modo pressoché continuo è l'energia acustica, come una resistenza che è percorsa dalla corrente trasmette all'ambiente energia termica.

Assumendo che il gas contenuto in un tubo si muova come un corpo rigido, quindi per velocità di volume abbastanza basse da non creare turbolenze e trascurando il moto non uniforme del gas vicino alle pareti del tubo, si assume che una pressione P mantenga il gas in moto a velocità uniforme secondo la legge:

P    =      Ra  *   u                3.4

da cui la definizione di Resistenza acustica

Ra   =     P  /   u                    3.5

Analogie preliminari

Dall'analogia formale fra le equazioni delle forze dissipative:

Re  =    V /  i        Rm  =   F / v        Ra   =   P /  u

possiamo stabilire perciò le analogie formali:

Tensione        <->    Forza         <->    Pressione                                         concetto di Potenziale

Corrente         <->    Velocità    <->   Velocità di volume                           concetto di Flusso

Sono analogie formali fra equazioni, fisicamente un corpo solido in moto non ha nulla a che vedere con gli elettroni in un conduttore o l'agitazione delle molecole di un gas, ma noi stiamo cercando un metodo di calcolo, non stiamo indagando sulla natura della realtà.

Potremmo anche fare la considerazione che i fenomeni meccanici ed i fenomeni acustici sono simili anche da un punto di vista fisico, ciò che fisicamente è totalmente diverso è il fenomeno elettrico, e noi stiamo proprio cercando di calcolare i sistemi meccanici ed acustici mediante un formalismo “elettrico”.

Partendo da un fenomeno semplice, la dissipazione, abbiamo compiuto il primo passo: ragionare per “analogie” può stare in piedi, se non altro da un punto di vista formale, che è proprio ciò che a noi interessa.


La Massa Acustica

Soffiare in un tubo corto e di sezione grande è più facile che soffiare in un tubo lungo e sottile: anche se il loro volume geometrico è lo stesso, e quindi la massa meccanica dell'aria contenuta nei tubi è la stessa, il comportamento dal punto di vista della pressione è diverso, cioè è diverso il comportamento acustico.

Ciò suggerisce che il concetto di massa acustica sia diverso da quello di massa meccanica, in quanto questa non dipende dalla geometria del tubo.

Tutti i conti tornano (risparmio i passaggi matematici) se la massa acustica si definisce come:

Ma    =     Mm /   S2                  4.1

Tenendo conto che la massa meccanica dell'aria contenuta nel tubo è  (Fig. 13):

Mm   =    ro  *   S   *   l                 4.2
   
dove   ro  è la densità dell'aria, S la sezione (superficie) del tubo e l la lunghezza del tubo, si ottiene

Ma     =     ( ro  *   l )   /   S            4.3

che ci dice che l'inerzia dell'aria contenuta nel tubo (detta anche inertanza in termini acustici)  è proporzionale alla lunghezza del tubo ed inversamente proporzionale alla sezione:  tutto torna con l'esperienza.

Un sistema elettrico oscillante

Vediamo ora un sistema non dissipativo, questa volta di natura elettrica.

Supponiamo di avere un condensatore ed un induttore, entrambi ideali (condensatore senza perdite e induttore con resistenza nulla) e carichiamo il condensatore collegandolo ad una batteria; quando il condensatore è carico lo stacchiamo dalla batteria e lo colleghiamo all'induttore, come in Fig. 14.


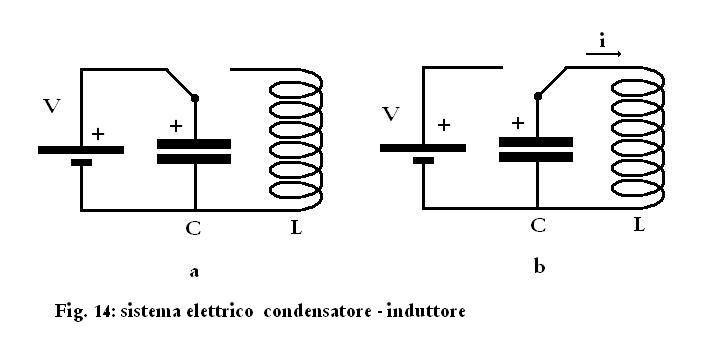
Nel primo passo (Fig. 14a) il condensatore ha accumulato una carica elettrica, che gli ha conferito energia potenziale.
Quando il condensatore è carico la tensione ai suoi capi è uguale a quella della batteria, non scorre più corrente e il condensatore conserva la sua carica (quindi la sua energia) anche quando viene scollegato dalla batteria; la sua energia è potenziale in quanto, in mancanza di corrente, non viene eseguito alcun lavoro.

Nel secondo passo (Fig. 14b) il condensatore inizia a scaricarsi attraverso l'induttore, ma la caratteristica dell'induttanza è di opporsi alle variazioni repentine di corrente, quindi la corrente cresce lentamente (se collegate i due capi del condensatore con un conduttore senza induttanza la corrente iniziale tende a infinito per la legge di Ohm).

Credo sia immediato riconoscere la somiglianza con l'esempio della molla e della massa di Fig. 3: tendendo la molla si carica di energia potenziale, la massa acquista velocità lentamente a causa della sua inerzia.

In Fig 15  è rappresentata l'evoluzione dello stato del sistema elettrico.

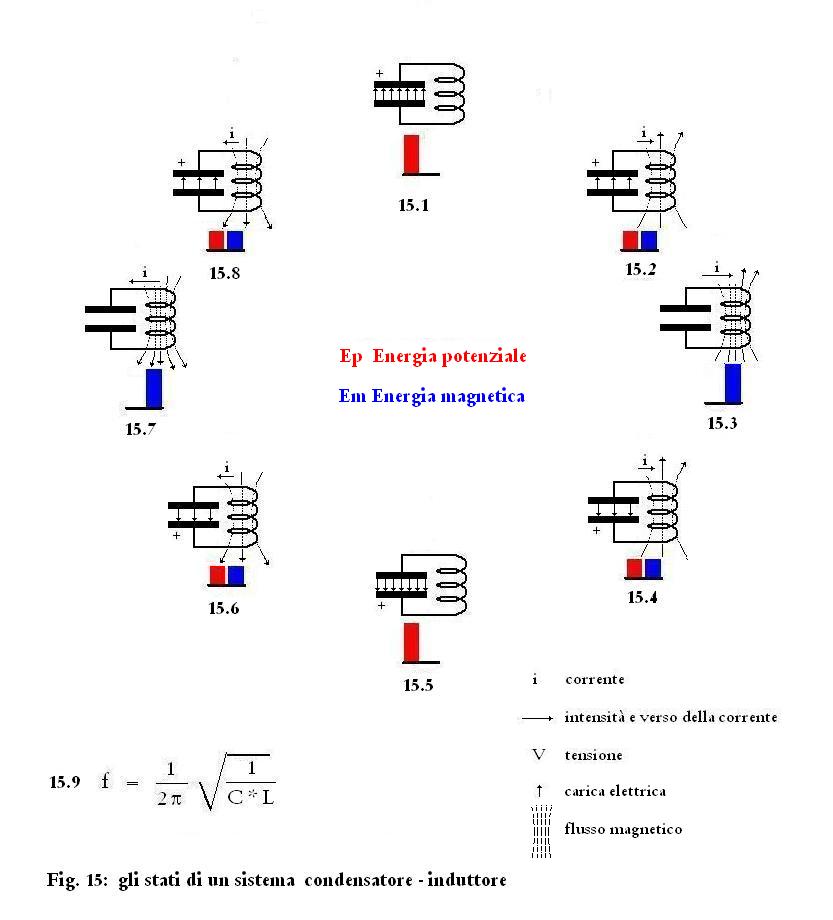
In 15.1  il condensatore è carico,  da 15.2 a 15.3  il condensatore si scarica attraverso l'induttore, cedendo energia potenziale, la corrente cresce creando un campo magnetico che raggiunge il massimo quando il condensatore è scarico, in 15.3, e l'energia magnetica è al massimo.
In un induttore la corrente non può variare istantaneamente, quindi continua a scorrere e carica il condensatore in verso opposto, in 15.5, dove si presenta la situazione iniziale con il segno elettrico invertito.
Quindi il processo si ripete fino a tornare alla condizione iniziale e ricomincia.
Anche qui la chiave è l'energia che si conserva: l'energia conferita al condensatore all'inizio non può sparire, in assenza di dissipazione, quindi si trasforma ciclicamente in potenziale prima e magnetica poi.

Si genera quindi una oscillazione, con la frequenza definita dalla Fig. 15.9.

Si vede immediatamente che la dinamica degli stati è esattamente uguale a quella della Fig. 4, il condensatore che accumula carica e quindi energia potenziale (elettrica) ha un comportamento analogo a quello della molla, che “accumula” spostamento e quindi energia potenziale (meccanica, elastica), l'induttore che si oppone al cambiamento istantaneo della corrente ed accumula energia magnetica si comporta come la massa che si oppone al cambiamento istantaneo di velocità ed accumula energia cinetica.

Le equazioni che definiscono le frequenze di risonanza hanno esattamente la stessa forma, se stabiliamo le analogie:

K     <->     1  /   C                               M      <->       L

Nella Fig. 16  si vede che, tenuto conto dei necessari cambiamenti di segno, la relazione fra la carica e la corrente è perfettamente analoga alla la relazione fra la velocità e lo spostamento di Fig. 5.

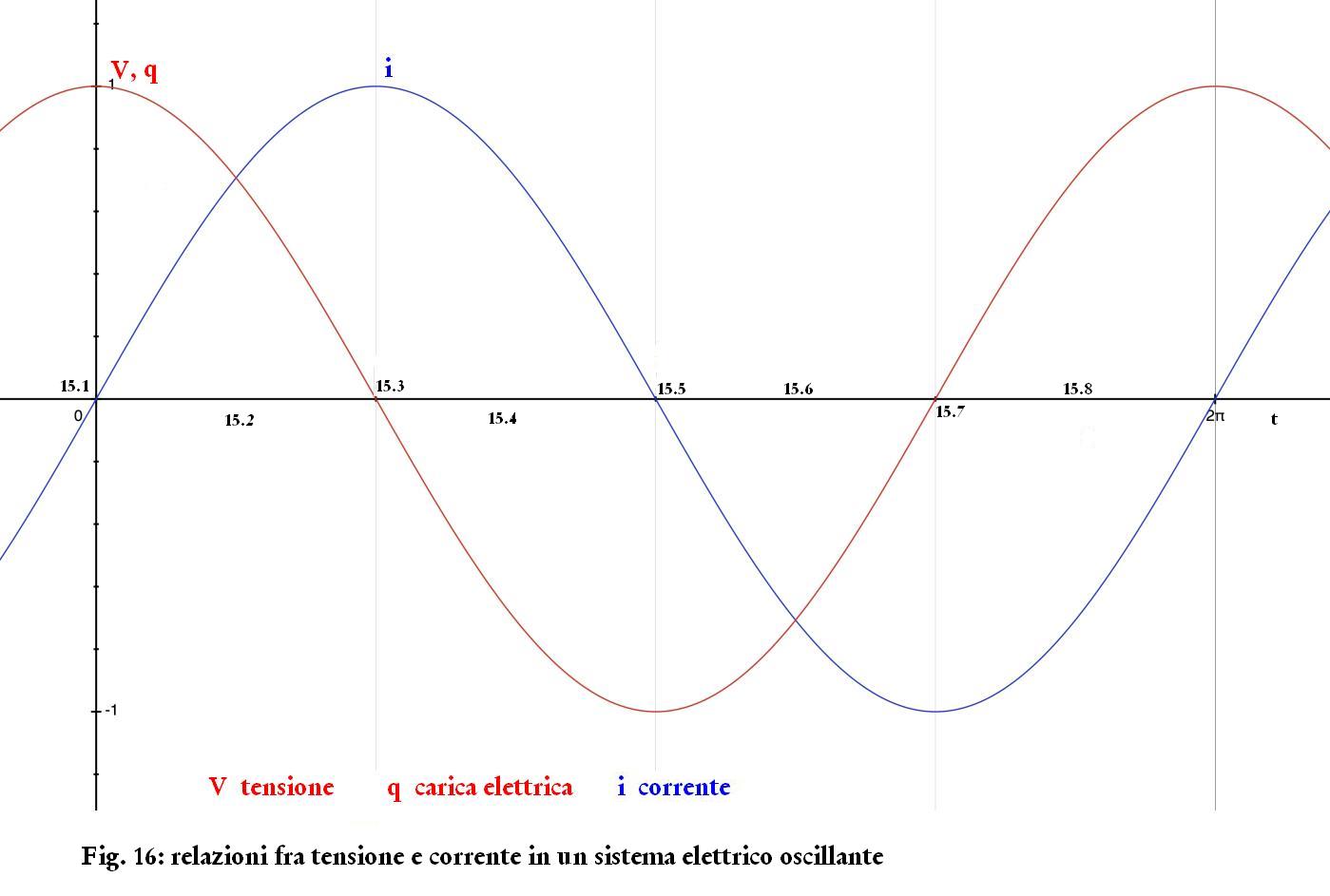
Abbiamo chiuso il cerchio, abbiamo visto che nel formalismo matematico le mele e le pere si equivalgono quindi si può analizzare qualche cosa fingendo che sia qualche cosa d'altro, se non si pretende di stabilire eguaglianze sostanziali.


Riassumiamo

La Fig. 17 riassume le leggi della dinamica dei tre sistemi



E'  evidente la somiglianza formale delle equazioni, che ci ha portato a stabilire l'analogia fra le variabili, riassunta in Fig 18.



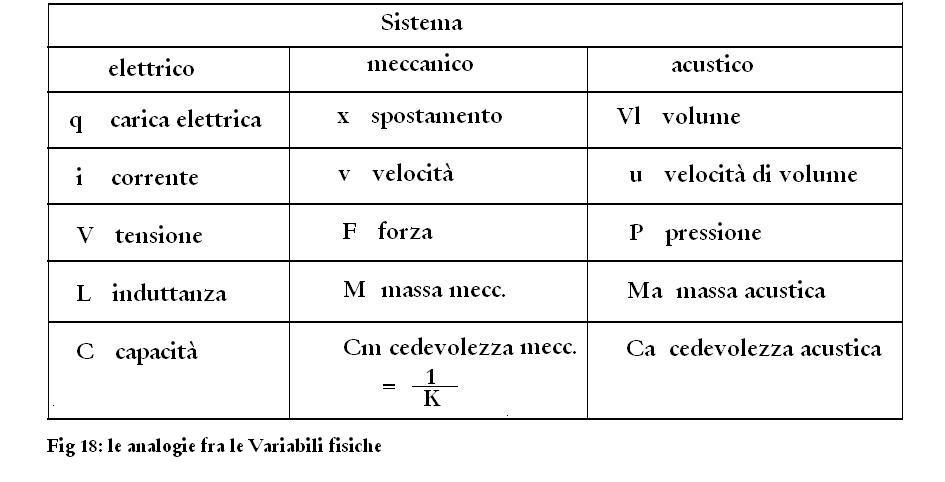
In Fig. 19 è riepilogato il comportamento dei sistemi dal punto di vista energetico:



Anche le equazioni dell'energia sono formalmente identiche.

I “Generatori” nei sistemi dissipativi

Fino ad ora abbiamo parlato di sistemi semplici, tranne in un caso: il caso del “moto armonico smorzato forzato” di Fig. 6, in cui abbiamo introdotto il concetto dell'energia “dissipata”.

Dal punto di vista dell'Energia, per qualsiasi sistema è valido il Principio di Conservazione dell'Energia, che stabilisce:

Ep + Ec + Ed =  Eg            5.1

la somma dell'Energia cinetica Ec, dell'Energia Potenziale Ep e dell'Energia ceduta all'ambiente Ed è uguale alla energia fornita dal generatore  Eg: l'energia ceduta all'ambiente può essere energia meccanica dissipata in attriti (quindi trasformata in calore), energia termica generata dalla corrente elettrica in un resistore oppure energia acustica.
In un diffusore tutti questi tipi di energia coesistono, ed il loro scopo è proprio una parte dell'energia dispersa.

Se torniamo per un momento al modello teorico di Fig. 1 vediamo che dobbiamo ancora esaminatre un elemento per arrivare alla fine.
I sistemi che ci interessa studiare sono sistemi che trasformano l'energia elettrica in energia acustica: sono sistemi diffusori che “suonano” perché ricevono un segnale elettrico da un “generatore”, che è l'amplificatore.

Il generatore è quindi l'elemento che manca per poter costruire modelli completi.

In Fig 20 sono riportati i tre modelli equivalenti di un diffusore bass reflex: i tre modelli  sono tratti da “Loudspeakers in Vented Boxes: Part I” di A. N. Thiele, e sono i modelli su cui sono basati la maggior parte dei simulatori.



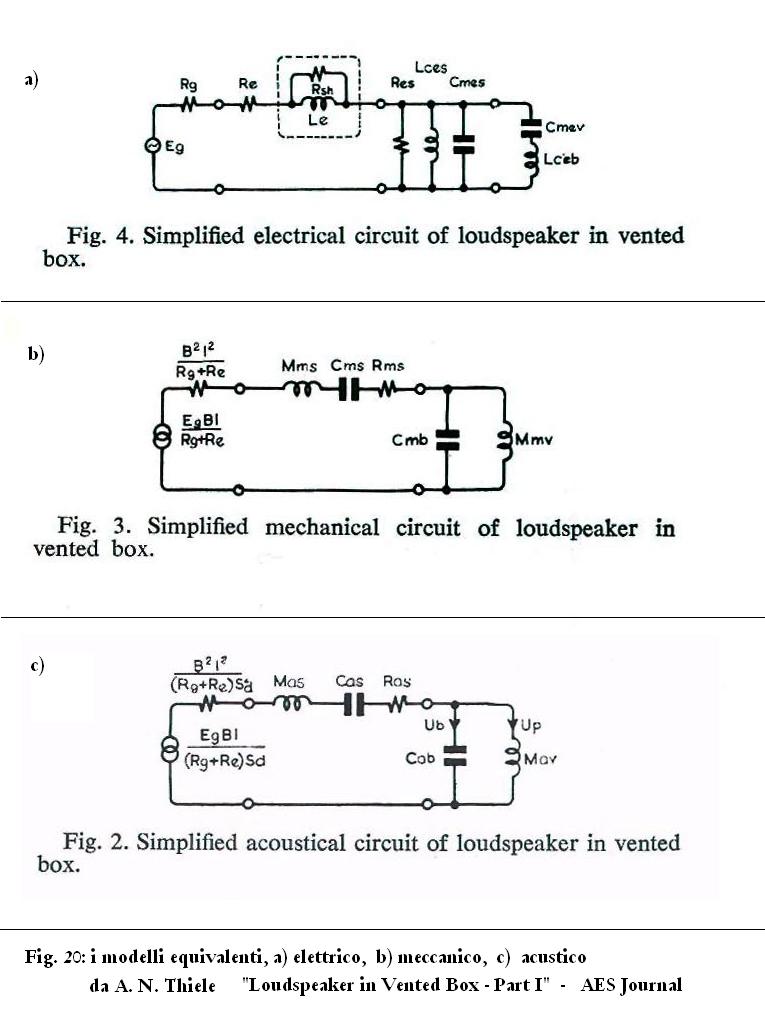
Concentriamoci sui generatori: 

Nel modello equivalente elettrico  (Fig. 20a) il generatore reale (il nostro amplificatore) è modellizzato mediante un generatore di tensione ideale,  Eg  , seguito dal resistore  Rg che rappresenta l'impedenza di uscita dell'amplificatore: è una approssimazione accettabile, dato che il modello totale è valido a frequenze basse ( < circa 400 Hz, in funzione del diametro del cono).

Nel modello equivalente meccanico (Fig. 20b) il generatore è espresso come:

 (  Eg    /    ( Rg + Re  ))   *     B*l            5.1     (ho semplicemente raggruppato i fattori)

dove il primo fattore (tra parentesi)  è una corrente  ed il secondo è il Fattore di Forza dell'altoparlante.

Quindi il generatore del modello meccanico è un generatore di Forza, e la Forza è l'analogo meccanico della Tensione.

Nel modello equivalente acustico (Fig. 20c) il generatore è espresso come:

 [(  Eg    /    ( Rg + Re  ))   *     B*l )]  /   S     5.2     (ho semplicemente raggruppato i fattori in modo opportuno )

dove il primo fattore (tra parentesi quadra),   è la Forza del modello meccanico  ed il secondo è la Superficie proiettata del cono  dell'altoparlante.

Quindi il generatore del modello acustico è un generatore di Pressione, e la Pressione è l'analogo acustico della Tensione.

Ora il cerchio è veramente chiuso: tutti gli elementi hanno i loro analoghi e possiamo modellizzare senza problemi.

Nei tre modelli presentati da Thiele, che sono perfettamente corrispondenti a quelli presentati da Small in “Vented-Box Loudspeaker System – Part I: small signal analysis”, una cosa salta all'occhio, o almeno dovrebbe: il circuito elettrico ha una topologia (cioè la disposizione dei componenti) diversa dai modelli meccanico ed acustico, che invece hanno topologie uguali.
La nostra analogia deve quindi essere applicata con un minimo di attenzione, in quanto per alcuni aspetti non si comporta come suggerirebbe l'intuizione, ma si può anche ragionare in modo diverso ed ottenere tre topologie identiche.

Attenti ai tranelli

Ad una analisi comparata dei circuiti equivalenti elettrico, meccanico ed acustico è immediatamente evidente è che ciò che nel circuito elettrico è in serie, nei circuiti meccanico ed acustico è in parallelo, mentre ciò che nel circuito elettrico è in parallelo,  nei circuiti meccanico ed acustico è in serie.

Per quanto ciò possa disorientarci, l'avevo in certo qual modo già anticipato quando avevo insistito sul fatto che tutto il ragionamento si basa sulla analogia formale fra le equazioni: il grande fisico Feynman disse che equazioni simili hanno soluzioni simili, ma ciò non implica che i fenomeni fisici che stanno sotto le equazioni siano effettivamente simili, pertanto non siamo autorizzati a spingere una analogia formale a stabilire analogie sostanziali.
Spesso sotto la matematica non c'è altro che matematica.
Torniamo sui nostri passi, e cerchiamo di capire che cosa, in una costruzione che era ragionevole e sembrava intuitivamente solida, ci porta ad un risultato che non è affatto intuitivo.

Perché il fatto che il circuito elettrico debba essere concettualmente “opposto” (serie diventa parallelo e viceversa) rispetto ai circuiti meccanico ed acustico è assolutamente corretto, nell'ambito e nei limiti del ragionamento che abbiamo fatto, ed il metodo di calcolo funziona perfettamente.
Dobbiamo solo stare molto attenti, quando trasformiamo uno schema nell'altro, a non farci trarre in inganno dall'analogia nella costruzione del “duale” (“duale” è il termine tecnico che esprime questo “essere opposto o speculare”, e che è solo apparente).

Procediamo per gradi.

In elettrodinamica valgono le leggi di Kirchoff, la legge delle correnti (KCL) e la legge delle tensioni (KVL).

KCL afferma che la somma algebrica delle correnti che confluiscono in un nodo (cioè che scorrono attraverso componenti uniti nel nodo) è zero.

KVL afferma che la somma algebrica delle differenze di potenziale ai capi di componenti che formano una maglia è zero.

Se ci trasferiamo al campo della meccanica e della dinamica dei fluidi, troviamo leggi analoghe,  che affermano che la somma algebrica delle forze, o delle pressioni, che agiscono su un corpo è zero e la somma algebrica delle velocità, o dei flussi (velocità di volume) in un punto è zero.
In realtà ciò è vero per i fluidi non comprimibili: la quantità di fluido che entra in un recipiente nell'unità di tempo deve essere uguale alla quantità che ne esce nello stesso tempo.

Per un gas ciò non è vero in termini generali, ma noi stiamo trattando sistemi acustici che operano in ambiente a pressione costante: sui tempi brevi rispetto al periodo dell'onda che ci interessa il fluido si comporta come se fosse non comprimibile.

Tutta la trattazione teorica del comportamento dell'aria nel condotto in un risuonatore di Helmholtz, come anche la trattazione del comportamento dell'aria in un contenitore chiuso, si basa su questo assunto: è una approssimazione non da poco, ma è esattamente ciò che si fa quando si afferma che i modelli su cui si basa la nostra analogia (e quindi, per inciso, tutti i modelli su cui sono basate le teorie di Novak, Beranek, Thiele e Small ecc) valgono per frequenza inferiori a 400 Hz per altoparlanti con diaframma da 15”, piuttosto che per dimensioni del condotto “piccole” rispetto alla lunghezza d'onda del suono alla frequenza di accordo del reflex ma “grandi abbastanza” per poter trascurare gli effetti di turbolenza lungo le pareti del condotto stesso.

In altre parole l'ambito in cui le analogie sono valide è nettamente definito, ed anche assai limitato, ed inoltre non è generalizzabile in modo indiscriminato.

Analogia meccanica: è intuitiva, ma fino a che punto?

Se accettiamo l'analogia che abbiamo definito prima, la forza si comporta come una tensione: una tensione “spinge” gli elettroni (la corrente) attraverso una resistenza, una forza spinge ad una data velocità un corpo soggetto ad un dato attrito: è molto intuitivo, la forza è come la tensione, l'attrito (resistenza meccanica) è come la resistenza elettrica, la corrente elettrica è come la velocità di spostamento.

Allo stesso modo la corrente che scorre in un induttore, e che tende a restare costante per il principio di conservazione dell'energia (in questo caso energia magnetica), si comporta come la velocità di un corpo di una data massa, che in assenza di vincoli ed attriti tende a restare costante per lo stesso principio di conservazione dell'energia (in questo caso energia cinetica).

E in modo simile una molla ed una cavità piena di aria si comportano come condensatori.

L'energia cinetica e l'energia magnetica sono entrambe legate al movimento (di una massa o di elettroni), e come abbiamo visto le equazioni dell'energia sono le stesse, come sono identiche tutte le equazioni che governano le velocità, le correnti, i flussi, le cariche, gli spostamenti, le forze, le pressioni ecc.

Ma se tutto è così “identico”, cos'è che può non funzionare? In realtà qualche cosa può non funzionare solo se cerchiamo di “forzare” l'analogia applicandola in modo meccanico, senza ragionare a fondo sulla natura reale dei fenomeni cui la applichiamo.

Il ragionamento da fare è articolato, e sarà condotto in due fasi successive.

Il primo passo è capire come si costruisce un modello meccanico ed acustico usando un formalismo elettrico. 

Il secondo passo consiste nell'analizzare le differenze fra il modello meccanico ed il modello elettrico dello stesso sistema (il modello acustico, come abbiamo già detto, è sostanzialmente simile al modello meccanico).

Come premessa al ragionamento parliamo di impedenze.
Fino ad ora ho parlato solo di Resistenze, che sono forze dissipative, e, almeno per la meccanica e l'elettricità, sono valide solo in regime continuo.
Quando si tratta di altoparlanti si ragiona invece nel dominio delle frequenze e non si parla più di sola resistenza, ma anche di Impedenza.

Per altro la definizione di impedenza dal punto di vista formale, quando espressa in modo sintetico, senza esplicitare le componenti reale ed immaginaria, è perfettamente identica a quella della resistenza:  nel caso elettrico abbiamo la seguente definizione

Ze =  V /  I                           6.1

che è la “fotocopia” della legge di Ohm, tranne che in questo caso i termini dipendono dalla frequenza, mentre nel caso meccanico abbiamo

Zm  =       Fm /  v                    6.2

che è la “fotocopia” della equazione 2.2.

L'impedenza di un componente ideale non dissipativo (un condensatore perfetto, una induttanza perfetta, un gas perfetto contenuto in una cavità dalle pareti perfettamente rigide senza scambio termico e senza turbolenze ecc) è non dissipativa: in altre parole non esiste la componente resistiva (o la parte reale dell'espressione analitica).

I sistemi reali sono sempre parzialmente dissipativi, quindi qualsiasi Impedenza (elettrica, meccanica, acustica) contiene una parte dissipativa.
A titolo di  esempio, limitandoci all'esempio elettrico, l'impedenza di un circuito risonante serie ideale è esattamente zero alla frequenza di risonanza, mentre in un circuito reale non è zero (è pari per lo meno alla resistenza ohmica dell'induttore reale con cui è costruito il circuito risonante).

Nel seguito i grafici di impedenze saranno sempre quelli di sistemi reali, anche quando i circuiti equivalenti alla base del ragionamento sono circuiti ideali.

Esempio meccanico

Nel corso della prima puntata avevo specificato, nell'esempio del mestolo e dei due elastici, che dovevano essere in parallelo, non in serie.

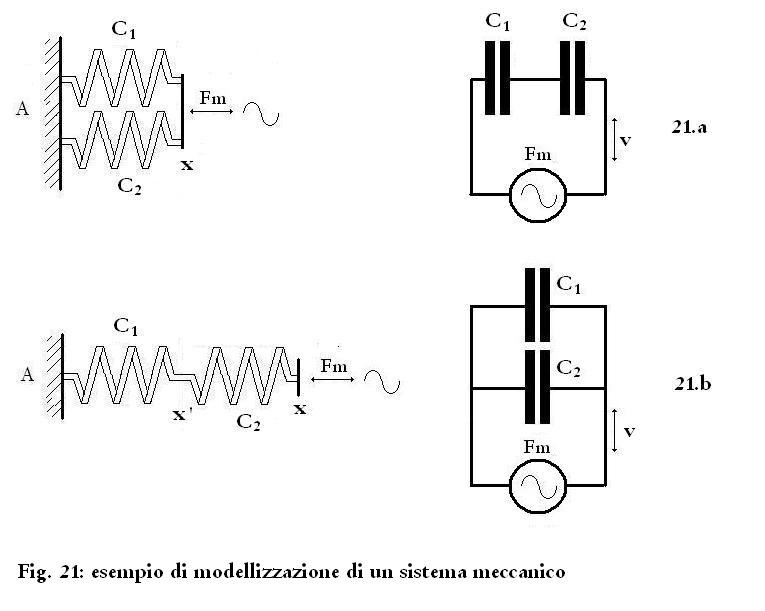
Partiamo con questo esempio: in Fig. 21.a vediamo due molle C1 e C2 collegate in parallelo, un capo ad un riferimento fisso (la “terra”), l'altro capo fissato ad un riferimento rigido che è tenuto in movimento vibratorio da una forza oscillante Fm.

Nel nostro sistema di analogie abbiamo stabilito che lo spostamento si comporta come la carica, la velocità come la corrente,  la forza come la tensione e la molla come un condensatore.

Il punto x si muove sotto l'azione della forza, ed è chiaro, avendo stabilito che il riferimento è rigido, che l'allungamento delle due molle è uguale e che il punto x ha la stessa velocità per ambedue le molle: stessa velocità = stessa corrente quindi nel circuito equivalente meccanico, che abbiamo costruito usando il formalismo elettrico, i due condensatori, per la Legge di Kirchoff delle correnti, sono in serie.

Controprova: nell'esempio di Fig. 21.b  le molle sono in serie.
La forza in tutti i punti del sistema meccanico è uguale: nel nostro esempio ideale non ci sono forze dissipative e quindi la molla si allunga fino a che la forza elastica uguaglia la forza esterna applicata: ogni molla trasmette al secondo estremo la forza applicata al primo e pertanto al punto x' la forza è la stessa che al punto x.

Lo spostamento in x' è ovviamente minore dello spostamento in x, e di conseguenza le velocità sono diverse.
Quindi stessa forza = stessa tensione ma correnti diverse, quindi per le leggi di Kirchoff i due condensatori del circuito equivalente meccanico, costruito con il formalismo elettrico, sono in parallelo.

Si può fare anche un'altra considerazione che porta allo stesso risultato: il condensatore non è equivalente alla costante elastica della molla, ma alla sua cedevolezza, che è l'inverso della costante elastica.

Una molla costituita da due molle in parallelo (Fig. 21.a) è più rigida, cioè ha una cedevolezza minore; una molla costituita da due molle in serie è più debole (lo stesso spostamento si ottiene con una forza minore), cioè la cedevolezza è maggiore.

Esempio acustico

Applichiamo lo stesso tipo di ragionamento ad un sistema acustico su cui ci siamo già soffermati: il risuonatore di Helmholtz  che abbiamo visto in Fig. 6.

Supponiamo una cavità con pareti rigide, con un tubo applicato ad una parete della cavità (il sistema cavità – tubo sia assolutamente rigido) ed un pistone senza massa ed in grado di muoversi senza attrito, applicato ad un'altra parete.

Applichiamo una pressione oscillante (un segnale acustico) al risuonatore, in due diversi scenari.

Supponiamo altresì che le dimensioni fisiche della cavità e del tubo siano piccole rispetto alla lunghezza d'onda generata dalla pressione oscillante che applicheremo, ma  le dimensioni trasversali del tubo siano abbastanza grandi da permetterci di trascurare la viscosità dell'aria nel suo movimento lungo la parete del tubo stesso (ancora approssimazioni).

Distinguiamo i due casi possibili, rappresentati in Fig. 22: la pressione oscillante viene applicata dal lato del tubo (Fig. 22.a) e la pressione oscillante viene applicata dal lato del pistone (Fig. 22.b).

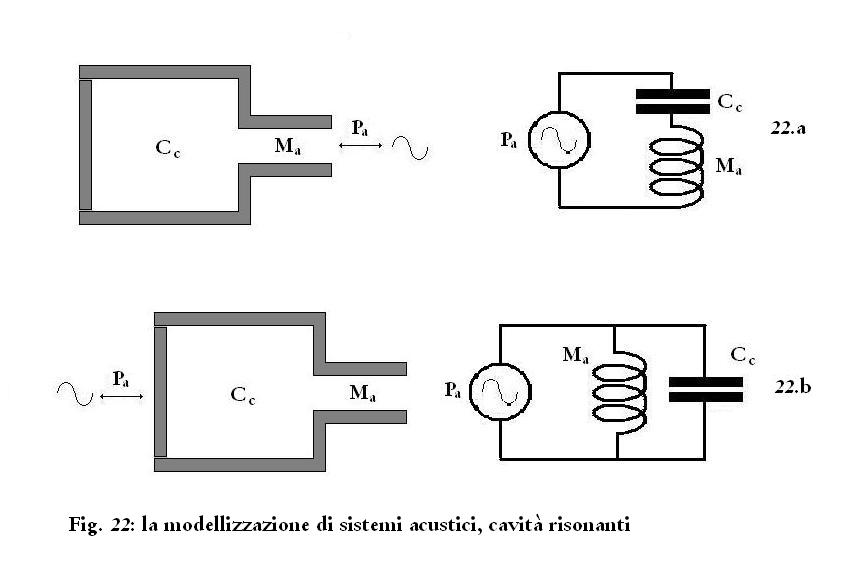
Nel primo caso (Fig. 22.a) il sistema si comporta come un tubo con due tratti con sezioni diverse: in questo caso la velocità di volume è la stessa per tutto il sistema (un altro nome per la “velocità di volume” è: “portata”), cioè per il tubo e per la cavità.

Nel circuito equivalente acustico la cavità è rappresentata dal condensatore, la massa dell'aria contenuta nel tubo dall'induttanza: l'analogo della corrente (cioè la velocità di volume) è la stessa e quindi i due elementi sono in serie.

Nel secondo caso (Fig. 22.b) la pressione agente sulla cavità e sul tubo è la stessa quindi i due elementi debbono essere messi in parallelo, nel  circuito equivalente acustico.

In entrambi i casi abbiamo un risonatore acustico, nel primo caso si ha una risonanza di portata, nel secondo caso una risonanza di pressione (detta anche antirisonanza).

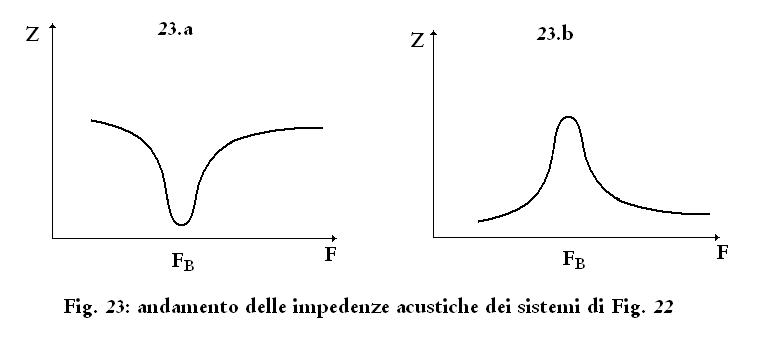
Il comportamento dei due sistemi è molto diverso: se analizziamo l'impedenza acustica troviamo che nel primo caso (Fig. 23.a) presenta un minimo alla frequenza di risonanza, come è ovvio per un circuito risonante serie, mentre nel secondo caso (Fig. 23.b) presenta un massimo, come è ovvio per un circuito risonante parallelo.

Il primo caso è quello del flauto, o della bottiglia che emette un suono quando soffiamo dentro il collo: in questo caso si eccita la risonanza dove l'impedenza acustica ha un minimo e quindi c'è il minor impedimento alla vibrazione dell'aria, che quindi si muove con la massima velocità (ed anche con il maggiore spostamento).

Il secondo caso è chiaramente simile ad un bass reflex: alla frequenza di risonanza, che è la frequenza di accordo della cassa, l'impedenza acustica è massima, quindi c'è il massimo impedimento al movimento del pistone (cioè del cono).

Quindi alla frequenza di accordo della cassa l'escursione del cono ha un minimo, mentre il movimento della massa d'aria contenuta nel tubo ha il massimo: in un diffusore reflex la pressione acustica emessa dal cono  ha un minimo alla frequenza di accordo della cassa e questo minimo di emissione è compensato dall'emissione acustica del tubo di accordo, che estende verso il basso l'emissione totale.

Un diffusore bass reflex reale è più complesso, in quanto il pistone ha massa ed è collegato alla cavità dalla sospensione, che è a sua volta una molla, e vi sono inoltre forze dissipative, quindi abbiamo non più uno ma due sistemi risonanti accoppiati sia meccanicamente che acusticamente, ma il principio di funzionamento è esattamente lo stesso.

La “dualità” meccanico-elettrica

Torniamo alla struttura di un altoparlante, rappresentata in Fig. 2, che può essere rappresentata in modo sintetico dalla Fig. 6, dove la forza Fm è quella generata dalla bobina mobile, la massa è quella del cono e la molla è la sospensione (ricordare la Fig. 1 aiuta a raccogliere le idee).

È facile rendersi conto che il sistema è equivalente a quello di Fig. 22.a: il primo è un sistema meccanico, il secondo è un sistema acustico, ed in entrambi i casi abbiamo una massa, una molla ed un generatore.

Il circuito equivalente è in entrambi i casi come quello di Fig. 22.a: un circuito risonante serie, che quindi presenta un minimo di impedenza (acustica e rispettivamente meccanica) alla frequenza di risonanza, come rappresentato in Fig. 23.a.

Quale è il comportamento elettrico del sistema?

La Fig. 7 ci può aiutare a capire: dato che l'impedenza acustica e meccanica hanno un minimo alla frequenza di risonanza (Fig. 23.a), la velocità di spostamento del cono ha invece un massimo alla frequenza di risonanza.

La velocità ha un massimo proprio perché alla frequenza di risonanza c'è minore opposizione al movimento: dalla 6.2 ricaviamo infatti che

v  =  Fm /  Zm

Se la velocità ha un massimo, anche le forze contro-elettromotrici generate dalla velocità dello spostamento del cono hanno un massimo, e dato che le forze contro-elettromotrici sono appunto di segno contrario alla forza elettromotrice prodotta dal generatore, la corrente assorbita alla risonanza ha un minimo.
Dove la corrente ha un minimo l'impedenza deve avere un massimo (la forza elettromotrice del generatore si suppone costante) e pertanto il circuito equivalente elettrico “deve” essere un circuito risonante parallelo.

Per un altoparlante in cassa chiusa il funzionamento è identico, con l'unica differenza che alla forza elastica della sospensione si aggiunge la forza elastica dell'aria contenuta nel box (meccanicamente in parallelo), quindi il sistema è analogo ad un altoparlante con sospensione più rigida.

In Fig. 24, tratta da “Closed-box Loudspeaker System” di Richard Small, vediamo riassunto quanto detto sopra.



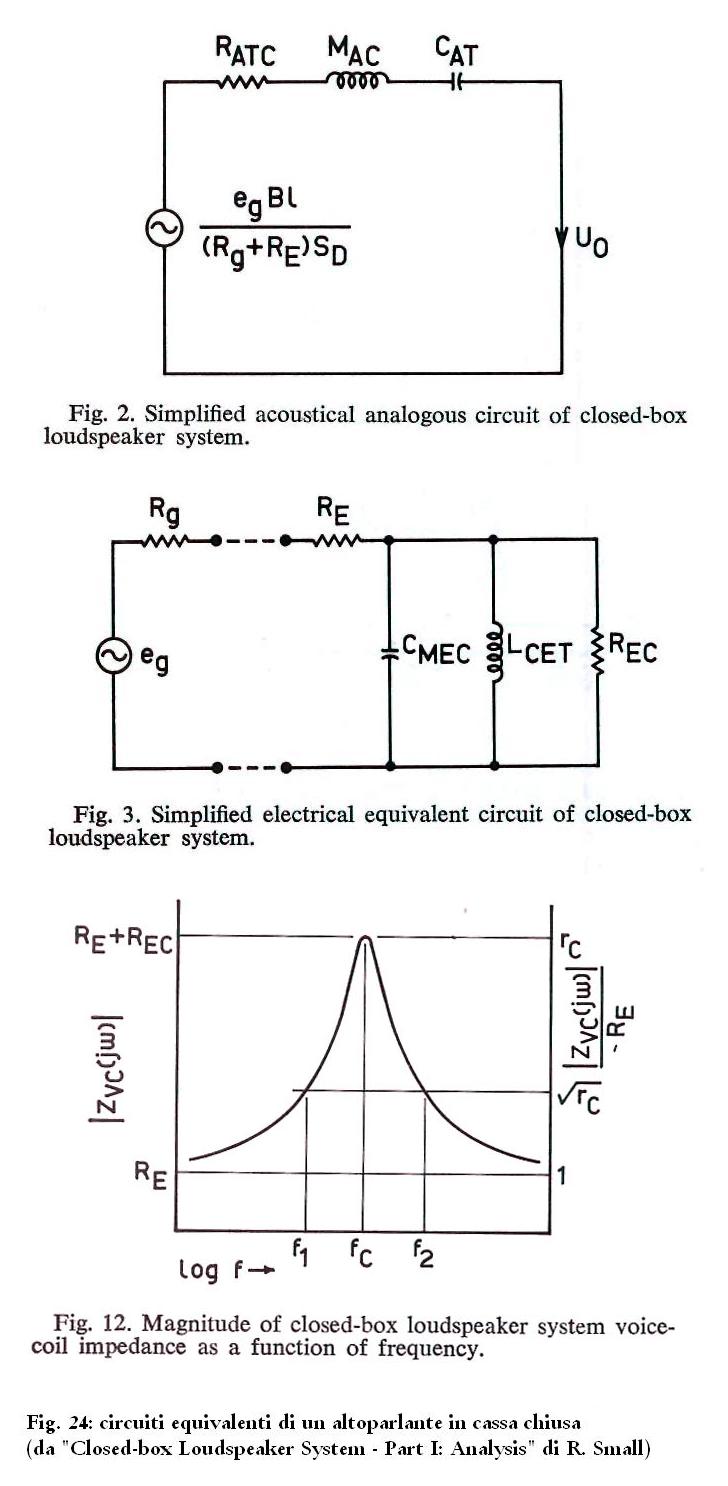
In base a queste considerazioni si giustifica il fatto che la topologia dei circuiti equivalenti sia diversa.

Per concludere, cambiamo prospettiva

Il ragionamento “per analogia” è un potente strumento per trattare sistemi diversi con formalismi simili, ed una volta che si sia assimilata la scomodità di avere topologie diverse, si sia imparato a costruire i “duali” e si abbiano ben presenti i principi fisici su cui si basano le analogie ed i loro limiti, tutto funziona perfettamente ed i nostri simulatori ci daranno ottimi risultati.
In linea di massima il circuito equivalente elettrico tratta impedenze, il circuito meccanico tratta escursioni ed il circuito acustico tratta pressioni acustiche (cioè curve di risposta).

Quindi tutto bene.

Ma se il cambio di topologia ci dà concettualmente fastidio? Se volessimo un modello unificato che in un unico circuito equivalente esprimesse impedenze, escursioni, pressioni?

C'è qualche altro modo di affrontare il problema?

Ciò che abbiamo visto finora va sotto il nome di “Analogia dell'impedenza” o “Analogia di Maxwell”, ed è basata sull'equivalenza che abbiamo stabilito fra Forza e Tensione, nella definizione dei potenziali, e fra Velocità e Corrente, nella definizione dei flussi.

Che cosa succede se decidiamo di usare equivalenze diverse? Innanzi tutto, è possibile usare equivalenze diverse?

L'analogia che abbiamo usato finora, con le sue equivalenze, è basata solo sulla analogie formali fra equazioni (l'ho ripetuto fino alla noia) e quindi qualsiasi analogia formale fra equazioni che non dia luogo a contraddizioni è altrettanto valida.

Definiamo quindi le seguenti equivalenze:

Velocità      <->    Portata (Velocità di Volume)      <-> Tensione                concetto di Potenziale
Forza         <->      Pressione                                     <-> Corrente                concetto di Flusso

Con queste equivalenze le equazioni base diventano quelle di Fig. 25:


e le variabili utilizzate cambiano:

Massa                 <->     Capacità

Forza elastica    <->    Induttanza

Ovviamente il cambiamento si ha solo nel sistema Elettrico, che è l'oggetto dell'analogia.

Mentre nel caso dell'analogia di Maxwell l'analogia del sistema elastico è stabilita fra la Cedevolezza della molla e la Capacità,  in questo caso l'analogia del sistema elastico è stabilita fra la Cedevolezza e l'Induttanza, ma il risultato è che due molle in parallelo si comportano come due induttanze in parallelo.

E' un risultato non da poco: con questo tipo di analogia la topologia dei circuiti equivalenti viene conservata.

È più difficile stabilire una somiglianza intuitiva fra Velocità e Tensione, come pure fra Forza e Corrente, rispetto alla somiglianza più “facile” dell'analogia di Maxwell, ma la conservazione della topologia rende più facile costruire i modelli equivalenti (sono tutti uguali) e soprattutto, venendo a mancare le “dualità” si può costruire un modello unico che esprima le proprietà elettriche, meccaniche ed acustiche, cioè costruire un unico circuito equivalente che rappresenti esattamente la Fig. 1.

Questo tipo di analogia è detto “Analogia della Mobilità” o “Analogia di Firestone”.

Conclusioni

Sicuramente qualcuno si sta chiedendo se tutto questo non sia una versione speciale del gioco delle tre carte.

La risposta sta tutta in quanto scritto all'inizio di questa puntata:

    “ equazioni simili hanno soluzioni simili”

e quello che noi stiamo cercando è un metodo di calcolo, non la natura ultima delle leggi fisiche.

Anche l'analogia di Firestone funziona perfettamente, e pur essendo meno intuitiva ha qualche vantaggio rispetto a quella di Maxwell.
Proprio perché stiamo cercando soluzioni di equazioni e non la natura nascosta delle leggi fisiche possiamo stabilire anche altri tipi di analogie, e purché si proceda con coerenza tutte possono funzionare e dare risultati corretti.

Ciò che non si deve dimenticare è che tutte le analogie sono formali, che non è lecito derivare proprietà sostanziali da analogie formali  (“ ... ciò non implica che i fenomeni fisici che stanno sotto le equazioni siano effettivamente simili...”) e soprattutto che l'ambito di funzionamento delle analogie e quindi dei modelli costruiti sulla base di esse è pesantemente limitato da tutte le approssimazioni fatte per costruirle.

.